


Next: Soluzione di alcuni degli
Up: Matematica Discreta (II modulo)
Previous: Lezione 21 (28 maggio
Subsections
Sia (T,r) un albero radicato, sull'insieme dei vertici si definiscono le
due relazioni 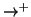 e
e 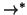 ,
ovvero la chiusura transitive e la
chiusura transitiva e riflessiva della relazione
,
ovvero la chiusura transitive e la
chiusura transitiva e riflessiva della relazione 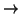 di
paternità
ponendo:
di
paternità
ponendo:
Proposizione 22.1
La relazione
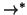
è un ordinamento parziale. E la relazione
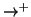
è
l'ordinamento stretto associato a
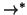
ossia
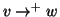
se e solo se
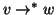
e
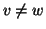
.
Dimostrazione.

Teorema 22.2
Sia (
T,
r) un albero radicato e per ogni
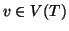
sia
P(
v) una
proposizione. Si supponga che:
- 1.
- P(r) sia vera;
- 2.
- per ogni
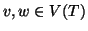 tali che
tali che 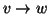 si ha che
si ha che
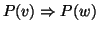
.
Allora
P(
v) è vera per ogni
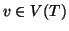
.
Teorema 22.3 (Induzione sugli alberi)
Sia (
T,
r) un albero radicato e per ogni
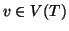
sia
P(
v) una
proposizione. Si supponga che:
- 1.
- P(r) sia vera;
- 2.
- per ogni
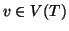 si ha che
si ha che
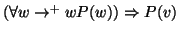 .
Allora P(v) è vera per ogni
.
Allora P(v) è vera per ogni 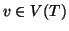 .
.
Dimostrazione.

Osservazione 22.4
Si osservi che nella dimostrazione del teorema precedente non si è mai usato
il fatto che si stesse parlando di alberi radicati, ma soltanto che
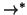
fosse un
ordinamento ben fondato ovvero che ogni successione
discendente ha minimo, e che tutto l'insieme dei vertici ha
un minimo rispetto a tale ordinamento. La stessa dimostrazione
può quindi essere usata per dimostrare il seguente teorema di induzione per
insiemi ben fondati.
Definizione 22.5
Sia
X un insieme e sia
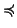
un ordinamento parziale su
X. Diremo
che
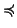
è
ben fondato se ogni successione discendente ha
minimo, ossia se per ogni
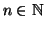
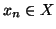
sono tali che
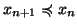
allora esiste un
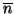
tale che
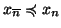
per ogni
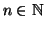
(in particolare se
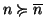
allora
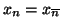
)).
Teorema 22.6 (Induzione ben fondata)
Sia
X un insieme e sia
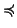
un ordinamento ben fondato su
X cha
ammette minimo
x0 (i.e.esiste
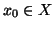
tale che
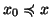
per
ogni
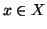
). Per ogni
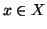
sia
P(
x) una proposizione. Si supponga
che:
- 1.
- P(x0) sia vera;
- 2.
- per ogni
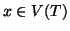 si ha che
si ha che
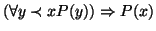 (dove
(dove 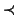 è una abbreviazione per
è una abbreviazione per
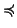 e
e 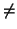 ).
).
Allora
P(
x) è vera per ogni
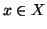
.
Domanda.
È vero che in un albero infinito esiste un ramo infinito?
Per ramo infinito intendiamo un cammino infinito (i.e. un sottografo isomorfo a
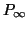 ).
).
In generale la risposta a questa domanda è negativa. Si consideri ad esempio
il grafo
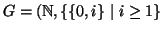 (vedi figura).
(vedi figura).
Figure 10:
Un contresempio al Lemma di König, senza l'ipotesi dei gradi finiti
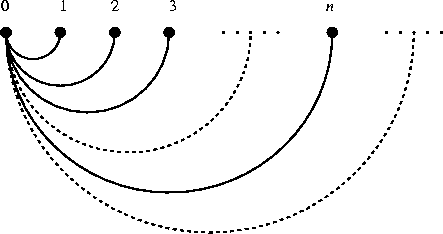 |
G è un albero. Infatti G è connesso dato che ogni vertice è
congiungibile al vertice 0. Inoltre se 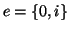 è un lato, allora
è un lato, allora
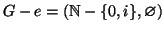 che è sconnesso. Quindi G è un albero per la
terza delle proprietà caratterizzanti degli alberi.
che è sconnesso. Quindi G è un albero per la
terza delle proprietà caratterizzanti degli alberi.
D'altra parte i cammini più lunghi che si possono trovare sono i cammini del
tipo (i,0,j) con 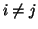 ,
che hanno lunghezza 2.
,
che hanno lunghezza 2.
Il problema sta nel fatto che nell'albero dell'esempio c'è un vertice di grado
infinito (su 0 arrivano infiniti lati). In effetti vale il seguente teorema:
Teorema 22.7 (Lemma di König)
Sia
T un albero infinito tale che ogni vertice ha
grado finito, allora
T ha rami infiniti.
Dimostrazione.
Fissiamo una radice r per T e sia 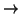 la relazione di paternità indotta
da tale radice. Costruiremo una funzione
la relazione di paternità indotta
da tale radice. Costruiremo una funzione
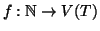 con la seguente
proprietà:
con la seguente
proprietà:
Chiaramente, una tale funzione risolve il problema.
Definiamo f ricorsivamente. Poniamo f(0)=r. Chiaramente i discendnti di
f(0) sono infiniti (tutti i vertici sono discendenti della radice).
Supponiamo di aver definito f(n) (che sia figlio di f(n-1) e che abbia una
discendenza infinita). Per ipotesi
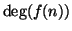 è finito, siano quindi
è finito, siano quindi
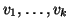 i figli di f(n) (i.e.
i figli di f(n) (i.e.
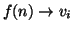 ). Per ogni
). Per ogni
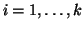 sia
sia
Chiaramente
Pertanto esiste un i tale che
Vi è infinito. Basta allora porre
f(n+1)=vi. Chiaramente
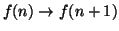 e la discendenza di f(n+1), che è Vi, è infinita.
e la discendenza di f(n+1), che è Vi, è infinita.




Next: Soluzione di alcuni degli
Up: Matematica Discreta (II modulo)
Previous: Lezione 21 (28 maggio
Domenico Luminati
2001-06-18
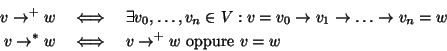
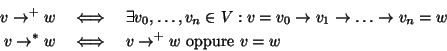
![]()
![]()
![]() ).
).
![]() (vedi figura).
(vedi figura).
![]() è un lato, allora
è un lato, allora
![]() che è sconnesso. Quindi G è un albero per la
terza delle proprietà caratterizzanti degli alberi.
che è sconnesso. Quindi G è un albero per la
terza delle proprietà caratterizzanti degli alberi.
![]() ,
che hanno lunghezza 2.
,
che hanno lunghezza 2.
![]() la relazione di paternità indotta
da tale radice. Costruiremo una funzione
la relazione di paternità indotta
da tale radice. Costruiremo una funzione
![]() con la seguente
proprietà:
con la seguente
proprietà:
![]() è finito, siano quindi
è finito, siano quindi
![]() i figli di f(n) (i.e.
i figli di f(n) (i.e.
![]() ). Per ogni
). Per ogni
![]() sia
sia