As a result of the VMC calculation one obtains a variational esimator for a
quantity (let it be described by an operator ![]() ), which corresponds to an
average over the trial wave function
), which corresponds to an
average over the trial wave function ![]() :
:
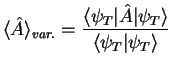 |
(2.157) |
Instead, the DMC method asymptotically provides a more precise mixed
estimator, which we denote as
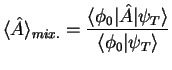 |
(2.158) |
Still, this type of average can differ from the ``pure'' ground state average,
which corresponds to the true quantum-mechanical equilibrium value at a zero
temperature
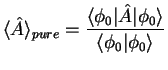 |
(2.159) |
The DMC method gives an exact result for the energy, as the mixed average of the
local energy
![]() coincides with the pure estimator.
This can be easily seen by noticing that when
coincides with the pure estimator.
This can be easily seen by noticing that when
![]() acts on
acts on ![]() , it
gives exactly the ground state energy.
, it
gives exactly the ground state energy.
We will show that averages of local operators can be calculated in a ``pure'' way.
This means that the pair distribution function, radial distribution, size of the
condensate can be found essentially exactly. We assume that
![]() . The ``pure'' average can be related to
the mixed one in the following way
. The ``pure'' average can be related to
the mixed one in the following way
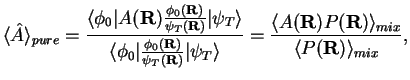 |
(2.160) |
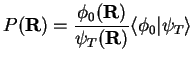 |
(2.161) |
One of important examples of a non-local quantity is the non-diagonal element of the one-body density matrix (see (2.141)). This quantity deserves a special attention, so we will explain an extrapolation technique, which can be applied for finding averages of a non-local operators.
Let us denote the difference between the trial wave function and ground-state wave
function as ![]()
| (2.162) |
Then the ground-state average can be written as
| (2.163) |
If ![]() is small the second order term
is small the second order term
![]() can be neglected.
After substitution
can be neglected.
After substitution
![]() the extrapolation formula becomes
the extrapolation formula becomes
It is possible to write another extrapolation formula of the same order of
accuracy:
Of course, if the extrapolation technique is applicable, formulae (2.164) and (2.165) give the same result. The second formula is preferable for extrapolation of a non-negative quantity (e.g. the OBDM), if the function can be very close to zero, as (2.165) preserves the sign of the function.
In the end of this Section we will mention that it can be proven that the measurement of the superfluid density in DMC method is a pure estimator and to a large extent is not biased by the chose of a trial wave function [Ast01,AG02].