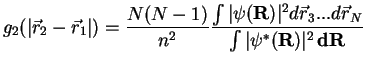 |
(2.152) |
The pair distribution function (TBDM) in a homogeneous system is given by the
formula (1.19)
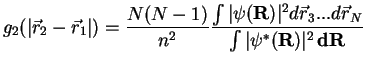 |
(2.152) |
Let us explain now how this formula is implemented in Monte Carlo calculation. We
make summation over all pairs of particles:
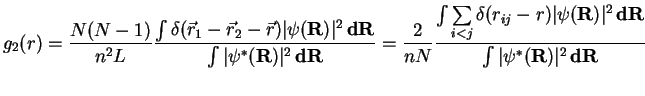 |
(2.153) |
If we do a discretization of the coordinate with spacing ![]() and introduce function
and introduce function
![]() which is one if
which is one if ![]() and zero otherwise, do summation over absolute value (the distribution is obviously symmetric) we obtain following
expressions:
and zero otherwise, do summation over absolute value (the distribution is obviously symmetric) we obtain following
expressions:
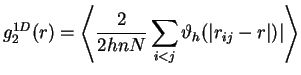 |
(2.154) |
In a uncorrelated system
![]() is constant and
is constant and ![]() .
.
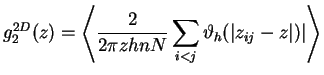 |
(2.155) |
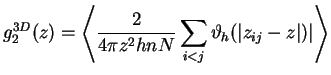 |
(2.156) |