In the construction of the trial function the antisymmitrization is included through
the Slater determinant
![]()
Thus at the variational trial move one has to calculate the ratio of two
determinants in addition to usual one- and two- body correlation terms present in
the bosonic VMC algorithm (compare with (2.37) and see Sec. 2.2).
An element of the Slater matrix is given by
![]() , where
, where
![]() is a single particle orbital. In
further latin indices will always refer to particle number and the greek indices to
orbital number. During a trial move in which position of only one particle get
changed, just one row of the Slater matrix changes. This means that instead of a
direct calculation of the Slater determinant a more efficient method can be used.
Before doing the trial move one should calculate the inverse matrix
is a single particle orbital. In
further latin indices will always refer to particle number and the greek indices to
orbital number. During a trial move in which position of only one particle get
changed, just one row of the Slater matrix changes. This means that instead of a
direct calculation of the Slater determinant a more efficient method can be used.
Before doing the trial move one should calculate the inverse matrix
![]() such that
such that
![]() or in terms of the matrix elements
or in terms of the matrix elements
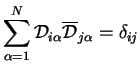 |
(2.93) |
If we denote the matrix with coordinate of the ![]() particle changed as
particle changed as ![]() then the ratio of interest becomes
then the ratio of interest becomes
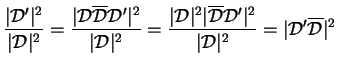 |
(2.94) |
The matrix
![]() is almost diagonal. Indeed, only
is almost diagonal. Indeed, only ![]() row is
different from the one of a unitary matrix. It means that the determinant of such a
matrix equals to the
row is
different from the one of a unitary matrix. It means that the determinant of such a
matrix equals to the ![]() element of this row, i.e.
element of this row, i.e.
After the move is accepted the inverse matrix must be updated. There is a fast way
of doing it. Instead of direct inversion of the determinant matrix one can use ![]() from eq.(2.95):
from eq.(2.95):
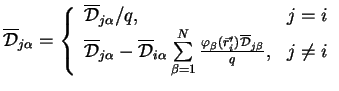 |
(2.96) |
Differentiating the trial wave function (2.92) one finds the expression for the
kinetic energy. It is equal to
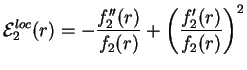 |
(2.98) |
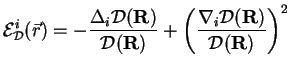 |
(2.99) |
The drift force (2.15) appearing in (2.97) is given by
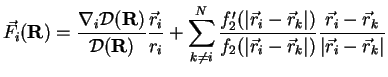 |
(2.100) |
The derivatives of the determinant are related to the derivatives of the orbitals in
an easy way (see formula (2.95))
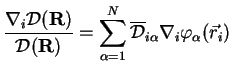 |
(2.101) |