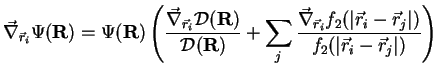Kinetic energy

We always use coordinate representation for the wave functions in our calculations, thus the calculation of the potential energy, which is diagonal in this representation, is trivial. Instead calculation of the kinetic energy demands knowledge of wave function derivatives. Let us calculate the first and second derivatives of the fermion wave function:

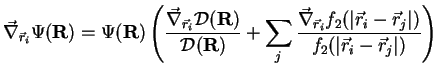$$\vec\nabla_{{\vec r}_i}\Psi({\bf R}) =\Psi({\bf R})\left( \frac{\... ...t{{\vec r}_i-{\vec r}_j}\vert)}{f_2(\vert{{\vec r}_i-{\vec r}_j}\vert)} \right)$$ (2.102)

$$\Delta_{{\vec r}_i}\Psi({\bf R}) =\Psi({\bf R}) \left( \left[ \fr... ... r}_i-{\vec r}_j}\vert)} \right]^2+ {\cal E}^{loc}_i + {\cal D}^{loc}_i \right)$$ (2.103)

The local energy is defined as

$${\cal E}^{loc}_i = \sum\limits_{j}\left[ \frac{\Delta_{{\vec r}_i}f_2(\vert{{\vec r}... ...r}_i-{\vec r}_j}\vert)}{f_2(\vert{{\vec r}_i-{\vec r}_j}\vert)}\right)^2\right]$$ (2.104)

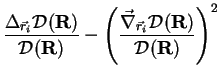$${\cal D}^{loc}_i = \frac{\Delta_{{\vec r}_i}{\cal D}({\bf R})}{{\cal D}({\bf R})}-\left(\frac{\vec\nabla_{{\vec r}_i}{\cal D}({\bf R})}{{\cal D}({\bf R})}\right)^2$$ (2.105)

The second derivative of the determinant is calculated explicitly, while the second derivative of the two-body Jastrow term is calculated by assuming spherical symmetry:

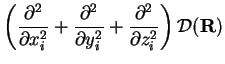$$\Delta_{{\vec r}_i}{\cal D}({\bf R}) = \left(\frac{\partial^2}{\partial x_i^2} +\frac{\partial^2}{\partial y_i^2} +\frac{\partial^2}{\partial z_i^2} \right){\cal D}({\bf R})$$ (2.106)

$$\Delta f_2(r) = f''_2(r)+\frac{2}{r}f'(r)$$ (2.107)