Dragg force

Now the projection of the force ${\bf F}$ onto the direction of motion ${\bf V}$ is given by the integral (7.29)

$$F^{2D}_V = -\frac{4i{g_{i}}^2\phi_0^2}{V} \int\limits_0^\infty\in... ...rac{k}{\sqrt{1-\cos^2\vartheta}} \frac{dk\,d\!\cos\vartheta}{(2\pi)^2} = \qquad$$ (7.32)

$$=\!-\!\frac{i{g_{i}}^2\phi_0^2}{4\pi^2 mV^2} \int\limits_0^\infty... ...)/2mV^2}}\right)\!\! \frac{k^2\,dk\,d\!\cos\vartheta}{\sqrt{1-\cos^2\vartheta}}$$

In the following we will introduce a two-dimensional density $n_{2D} = N/L^2$. The square of the unperturbed homogeneous solution equals to it $\phi_0^2 = n_{2D}$. The integral (7.32) is different from zero only if integrand has poles, which means that the velocity $V$ must be larger than the speed of sound $c$. Only momenta smaller than $k_{max}$ (see eq.(7.26)) contribute to the integral

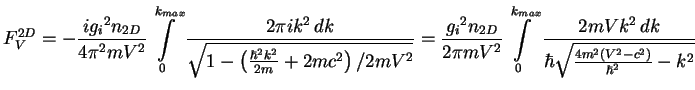$$F^{2D}_V = -\frac{i{g_{i}}^2n_{2D}}{4\pi^2mV^2} \int\limits_0^{k_... ..._0^{k_{max}} \frac{2mV k^2\,dk} {\hbar\sqrt{\frac{4m^2(V^2-c^2)}{\hbar^2}-k^2}}$$ (7.33)

We recall simple integral equality $\int_0^\varkappa\frac{k^2\,dk}{\sqrt{\varkappa^2-k^2}}=\frac{\pi}{4}\varkappa^2$ and finally have

$$F^{2D}_V = \frac{{g_{i}}^2 n_{2D}}{\hbar^3V}(V^2-c^2).$$ (7.34)

In a quasi two-dimensional system, i.e. when the gas is confined in the $z$-direction by the harmonic potential $m\omega_z^2z^2/2$, the two-dimensional coupling constant equals (see 1.122)

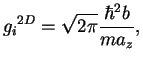$${g_{i}}^{2D}=\sqrt{2\pi}\frac{\hbar^2b}{ma_z},$$ (7.35)

where $a_z=\sqrt{\hbar/m\omega_z}$ is the oscillator length and $b$ is the three-dimensional scattering length. We consider here only the mean-field $2D$ situation. See [PS03],§17 and [PGS04] for a more detail discussion.

Notice again that our calculations do not take into account creation of vortex pairs which is possible at $V<c$.