| (7.21) |
The force with which the impurity acts on the system is
| (7.21) |
Expanding the wave function into the sum of ![]() and
and ![]() and neglecting
terms of order
and neglecting
terms of order ![]() we obtain
we obtain
It is convenient to do the integration in spherical coordinates with ![]() being angle between
being angle between ![]() and
and ![]() . There is no dependence on the angle
. There is no dependence on the angle ![]() and it can be immediately integrated out
and it can be immediately integrated out
The ![]() -function can be further developed
-function can be further developed
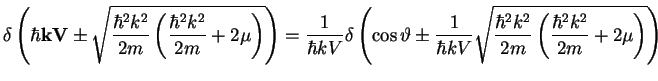 |
(7.25) |
The poles in the integration over ![]() appear if the square root in the
denominator is smaller than one, which leads to the restriction on the values of
momentum which contribute
appear if the square root in the
denominator is smaller than one, which leads to the restriction on the values of
momentum which contribute
Thus the energy dissipation takes place only if the impurity moves with a speed larger than the speed of sound.
Let us calculate the projection ![]() of the force
of the force ![]() to the direction
to the direction ![]() of the movement of the perturbation. It means that we have to multiply formula
(7.23) on
of the movement of the perturbation. It means that we have to multiply formula
(7.23) on ![]()
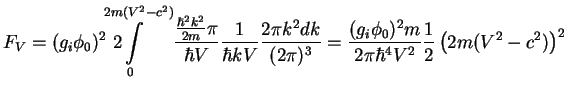 |
Now we can use that square of the unperturbed wave function gives the density
![]() and the coupling constant can be expressed as
and the coupling constant can be expressed as
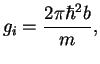 |
(7.27) |
Finally, we obtain following expression for the projection of the force
The energy dissipation,
![]() , can be evaluated by measuring the heating
of the gas.
, can be evaluated by measuring the heating
of the gas.
For large ![]() the force is proportional to
the force is proportional to ![]() . The energy dissipation per unit
time can then be presented as
. The energy dissipation per unit
time can then be presented as
![]() with the damping rate
with the damping rate
![]()
Note in conclusion that our perturbative calculations can not describe processes
involving dissipation of energy due to creation of quantized vortex rings. Such a
creation is possible at ![]() but has a small probability for low velocity and for a
weak point-like impurity.
but has a small probability for low velocity and for a
weak point-like impurity.