Consider two interacting mass ![]() bosons with position vectors
bosons with position vectors ![]() and
and
![]() , where
, where
![]() , in a waveguide with harmonic
confinement in the radial direction. If we introduce the center of mass coordinate
, in a waveguide with harmonic
confinement in the radial direction. If we introduce the center of mass coordinate
![]() and the relative coordinate
and the relative coordinate
![]() , the problem
separates. Since the solution to the center of mass Hamiltonian is given readily,
we only consider the internal Hamiltonian
, the problem
separates. Since the solution to the center of mass Hamiltonian is given readily,
we only consider the internal Hamiltonian ![]() , which can be conveniently
written in terms of cylindrical coordinates
, which can be conveniently
written in terms of cylindrical coordinates
![]() ,
,
Considering a regularized zero-range pseudo-potential
![]() , where
, where ![]() denotes the
3D scattering length, Olshanii [Ols98] derives an effective 1D Hamiltonian,
denotes the
3D scattering length, Olshanii [Ols98] derives an effective 1D Hamiltonian,
Olshanii's result shows that the waveguide gives rise to an effective interaction,
parameterized by the coupling constant ![]() , which can be tuned to any strength
by changing the ratio between the 3D scattering length
, which can be tuned to any strength
by changing the ratio between the 3D scattering length ![]() and the transverse
oscillator length
and the transverse
oscillator length ![]() .
.
The renormalized coupling constant, Eq. 4.3, can be compared with the
unrenormalized coupling constant ![]() (1.124),
(1.124),
Figure 4.1 shows the unrenormalized coupling constant ![]() [dashed
line, Eq. 4.6] together with the renormalized coupling constant
[solid line, Eq. 4.3]. For
[dashed
line, Eq. 4.6] together with the renormalized coupling constant
[solid line, Eq. 4.3]. For
![]() , the renormalized
coupling constant
, the renormalized
coupling constant ![]() is nearly identical to the unrenormalized coupling
constant
is nearly identical to the unrenormalized coupling
constant ![]() . For large
. For large ![]() , however, the confinement induced
renormalization becomes important, and the effective 1D coupling constant
, however, the confinement induced
renormalization becomes important, and the effective 1D coupling constant ![]() ,
Eq. 4.3, has to be used. At the critical value
,
Eq. 4.3, has to be used. At the critical value
![]() (indicated by a vertical arrow in Fig. 4.1),
(indicated by a vertical arrow in Fig. 4.1), ![]() diverges.
For
diverges.
For
![]() ,
, ![]() reaches an asymptotic value,
reaches an asymptotic value,
![]() (indicated by a horizontal arrow in
Fig. 4.1). Finally,
(indicated by a horizontal arrow in
Fig. 4.1). Finally, ![]() is negative for all negative 3D scattering
lengths. The inset of Fig. 4.1 shows the effective 1D scattering length
is negative for all negative 3D scattering
lengths. The inset of Fig. 4.1 shows the effective 1D scattering length
![]() , Eq. 4.5, as a function of
, Eq. 4.5, as a function of ![]() . For small positive
. For small positive
![]() ,
, ![]() is negative and it changes sign at
is negative and it changes sign at
![]() (
(![]() for
for
![]() ). Moreover,
). Moreover, ![]() reaches, just as
reaches, just as ![]() , an asymptotic
value for
, an asymptotic
value for
![]() ,
,
![]() (indicated by a
horizontal arrow in the inset of Fig. 4.1). The renormalized 1D scattering
length
(indicated by a
horizontal arrow in the inset of Fig. 4.1). The renormalized 1D scattering
length ![]() is positive for negative
is positive for negative ![]() , and approaches
, and approaches ![]() as
as
![]() . Figure 4.1 suggests that tuning the 3D scattering
length
. Figure 4.1 suggests that tuning the 3D scattering
length ![]() to large values allows a universal quasi-one dimensional regime,
where
to large values allows a universal quasi-one dimensional regime,
where ![]() and
and ![]() are independent of
are independent of ![]() , to be entered.
, to be entered.
![\includegraphics[height=11cm,width=0.6\columnwidth]{jpb1.eps}](jpb1.gif) |
The effective coupling constant ![]() , Eq. 4.3, has been derived
for a wave guide geometry, that is, with no axial confinement. However, it also
describes the scattering between two bosons confined to other quasi-one dimensional geometries.
Consider, e.g., a Bose gas under harmonic confinement. If the confinement in the
axial direction is weak compared to that of the radial direction, the scattering
properties of each atom pair are expected to be described accurately by the
effective coupling constant
, Eq. 4.3, has been derived
for a wave guide geometry, that is, with no axial confinement. However, it also
describes the scattering between two bosons confined to other quasi-one dimensional geometries.
Consider, e.g., a Bose gas under harmonic confinement. If the confinement in the
axial direction is weak compared to that of the radial direction, the scattering
properties of each atom pair are expected to be described accurately by the
effective coupling constant ![]() and the effective scattering length
and the effective scattering length ![]() .
.
The internal motion of two bosons under highly-elongated confinement can be
described by the following 3D Hamiltonian
The corresponding 1D Hamiltonian reads
The 1D eigenenergies ![]() of the stationary Schrödinger equation,
of the stationary Schrödinger equation,
The energy ![]() , in turn, determines the internal 1D eigenenergies
, in turn, determines the internal 1D eigenenergies ![]() ,
,
In Eq. 4.11, ![]() denotes the characteristic oscillator length in the
axial direction,
denotes the characteristic oscillator length in the
axial direction,
![]() .
.
To compare the eigenenergies ![]() and
and ![]() , we use, for the 3D
atom-atom interaction potential
, we use, for the 3D
atom-atom interaction potential ![]() , a short-range (SR) modified
Pöschl-Teller potential (1.97)
, a short-range (SR) modified
Pöschl-Teller potential (1.97) ![]() that can support two-body bound states,
that can support two-body bound states,
In the above equation, ![]() denotes the well depth, and
denotes the well depth, and ![]() the range of the
potential. In our calculations,
the range of the
potential. In our calculations, ![]() is fixed at a value much smaller than the
transverse oscillator length,
is fixed at a value much smaller than the
transverse oscillator length,
![]() . To simulate the behavior of
. To simulate the behavior of
![]() near a field-dependent Feshbach resonance, we vary the well depth
near a field-dependent Feshbach resonance, we vary the well depth ![]() ,
and consequently, the scattering length
,
and consequently, the scattering length ![]() . It has been shown that such a
model describes many atom-atom scattering properties near a Feshbach resonance
properly [TWMJ00]. Figure 4.2 shows the dependence of the 3D
scattering length
. It has been shown that such a
model describes many atom-atom scattering properties near a Feshbach resonance
properly [TWMJ00]. Figure 4.2 shows the dependence of the 3D
scattering length ![]() on
on ![]() . Importantly,
. Importantly, ![]() diverges for particular
values of the well depth
diverges for particular
values of the well depth ![]() . At each of these divergencies, a new two-body
. At each of these divergencies, a new two-body
![]() -wave bound state is created. The inset of Fig. 4.2 shows the range of
well depths
-wave bound state is created. The inset of Fig. 4.2 shows the range of
well depths ![]() used in our calculations.
used in our calculations.
![\includegraphics[width=0.57\columnwidth]{jpb2.eps}](jpb2.gif) |
To benchmark our MC calculations (see Chapter 2 and Sec. 4.4),
we solve the 3D Schrödinger equation, Eq. 4.8, with ![]() for various well depths
for various well depths ![]() using a two-dimensional B-spline basis in
using a two-dimensional B-spline basis in ![]() and
and
![]() . Figure 4.3 shows the resulting 3D eigenenergies
. Figure 4.3 shows the resulting 3D eigenenergies ![]() (diamonds) as a function of the 3D scattering length
(diamonds) as a function of the 3D scattering length ![]() . We distinguish
between two sets of states:
. We distinguish
between two sets of states:
1) States with
![]() are referred to as gas-like
states; their behavior is, to a good approximation, characterized by the 3D
scattering length
are referred to as gas-like
states; their behavior is, to a good approximation, characterized by the 3D
scattering length ![]() , and is hence independent of the detailed shape of the
atom-atom potential. The energies of the gas-like states are shown in
Fig. 4.3(a).
, and is hence independent of the detailed shape of the
atom-atom potential. The energies of the gas-like states are shown in
Fig. 4.3(a).
2) States with
![]() are referred to as molecular-like
bound states; their behavior depends on the detailed shape of the atom-atom
potential. The energies of these bound states are shown in Fig. 4.3(b). The
well depth
are referred to as molecular-like
bound states; their behavior depends on the detailed shape of the atom-atom
potential. The energies of these bound states are shown in Fig. 4.3(b). The
well depth ![]() of the short-range interaction potential
of the short-range interaction potential ![]() is chosen such
that
is chosen such
that ![]() supports -- in the absence of the confining potential -- no
supports -- in the absence of the confining potential -- no
![]() -wave bound state for
-wave bound state for ![]() , and one
, and one ![]() -wave bound state for
-wave bound state for ![]() .
Figure 4.3(b) shows that the bound state remains bound for
.
Figure 4.3(b) shows that the bound state remains bound for
![]() and for negative
and for negative ![]() if tight radial confinement is
present. In addition, a dashed line shows the 3D binding energy,
if tight radial confinement is
present. In addition, a dashed line shows the 3D binding energy,
![]() , which accurately describes the highest-lying molecular bound state in
the absence of any external confinement if
, which accurately describes the highest-lying molecular bound state in
the absence of any external confinement if ![]() is much larger than the range
is much larger than the range
![]() of the potential
of the potential ![]() .
.
The B-spline basis calculations yield not only the internal 3D eigenenergies
![]() , but also the corresponding wave functions
, but also the corresponding wave functions
![]() . The
nodal surface of the lowest-lying gas-like state, which is to a good approximation
an ellipse in the
. The
nodal surface of the lowest-lying gas-like state, which is to a good approximation
an ellipse in the ![]() -plane, is a crucial ingredient of our many-body
calculations. Section 4.4 discuss in detail how this nodal surface is used
to parametrize our trial wave function entering the MC calculations.
-plane, is a crucial ingredient of our many-body
calculations. Section 4.4 discuss in detail how this nodal surface is used
to parametrize our trial wave function entering the MC calculations.
To compare the energy spectrum for ![]() of the effective 1D Hamiltonian with that
of the 3D Hamiltonian, Fig. 4.3 additionally shows the 1D eigenenergies
of the effective 1D Hamiltonian with that
of the 3D Hamiltonian, Fig. 4.3 additionally shows the 1D eigenenergies
![]() (solid lines) obtained by solving the Schrödinger equation for
(solid lines) obtained by solving the Schrödinger equation for
![]() , Eq. 4.9, semi-analytically [using the renormalized
coupling constant
, Eq. 4.9, semi-analytically [using the renormalized
coupling constant ![]() , Eq. 4.3]. Figure 4.3(a)
demonstrates excellent agreement between the 3D and the 1D internal energies for
all states with gas-like character. For positive
, Eq. 4.3]. Figure 4.3(a)
demonstrates excellent agreement between the 3D and the 1D internal energies for
all states with gas-like character. For positive ![]() , the effective 1D
Hamiltonian fails to reproduce the energy spectrum of the molecular-like bound
states of the 3D Hamiltonian accurately [see Fig. 4.3(b), and also
[BMO03,BTJ03]].
, the effective 1D
Hamiltonian fails to reproduce the energy spectrum of the molecular-like bound
states of the 3D Hamiltonian accurately [see Fig. 4.3(b), and also
[BMO03,BTJ03]].
![\includegraphics[width=0.8\columnwidth]{jpb3.eps}](jpb3.gif) |
Our main focus is in the lowest-lying energy level with gas-like character. This
energy branch is shown in Fig. 4.3(c) on an enlarged scale. A horizontal
dashed line shows the lowest internal 3D eigenenergy for two non-interacting
spin-polarized fermions (where the anti-symmetry of the wave function enters in the
![]() coordinate). Our numerical calculations confirm [BMO03] that for
coordinate). Our numerical calculations confirm [BMO03] that for
![]() (
(
![]() ) the two boson system behaves as if
it consisted of two non-interacting spin-polarized fermions (TG gas). The energy
) the two boson system behaves as if
it consisted of two non-interacting spin-polarized fermions (TG gas). The energy
![]() is larger than that of two non-interacting fermions for
is larger than that of two non-interacting fermions for
![]() , and approaches the first excited state energy of two
non-interacting bosons for
, and approaches the first excited state energy of two
non-interacting bosons for
![]() [indicated by a dotted line in
Fig. 4.3(a)].
[indicated by a dotted line in
Fig. 4.3(a)].
For positive ![]() , the 1D Schrödinger equation, Eq. 4.10, does
not support molecular-like bound states. Consequently, the wave function of the
lowest-lying gas-like state is positive definite everywhere. For negative
, the 1D Schrödinger equation, Eq. 4.10, does
not support molecular-like bound states. Consequently, the wave function of the
lowest-lying gas-like state is positive definite everywhere. For negative ![]() ,
however, one molecular-like two-body bound state exists. If
,
however, one molecular-like two-body bound state exists. If ![]() the
bound-state wave function is approximately given by the eigenstate
the
bound-state wave function is approximately given by the eigenstate
![]() of the 1D Hamiltonian without confinement,
Eq. 4.2,
of the 1D Hamiltonian without confinement,
Eq. 4.2,
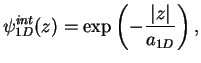 |
(4.15) |
For the highly-elongated trap with ![]() shown in Fig. 4.3(b) and
positive
shown in Fig. 4.3(b) and
positive ![]() the above binding energy nearly coincides with the exact
eigenenergy of the molecular-like bound state obtained from the solution of the
transcendental equation (4.11) (solid line). The two-body binding energy,
Eq. 4.16, is largest for
the above binding energy nearly coincides with the exact
eigenenergy of the molecular-like bound state obtained from the solution of the
transcendental equation (4.11) (solid line). The two-body binding energy,
Eq. 4.16, is largest for
![]() (
(
![]() ); in this case, the molecular-like bound state wave function
is tightly localized around
); in this case, the molecular-like bound state wave function
is tightly localized around ![]() , where
, where ![]() . Consider a system with
. Consider a system with
![]() . For negative
. For negative ![]() (positive
(positive ![]() ), the nodes along the
relative coordinate
), the nodes along the
relative coordinate ![]() of the lowest-lying gas-like wave function (in this case,
the first excited state) are then approximately given by
of the lowest-lying gas-like wave function (in this case,
the first excited state) are then approximately given by ![]() . Thus,
imposing the boundary condition
. Thus,
imposing the boundary condition
![]() at
at ![]() and
restricting the configuration space to
and
restricting the configuration space to ![]() allows one to obtain an
approximation to the eigenenergy of the first excited eigen state. Furthermore,
imposing the boundary condition
allows one to obtain an
approximation to the eigenenergy of the first excited eigen state. Furthermore,
imposing the boundary condition
![]() at
at ![]() is identical to
solving the 1D Schrödinger equation for a hard-rod interaction potential
is identical to
solving the 1D Schrödinger equation for a hard-rod interaction potential
![]() (1.79),
(1.79),
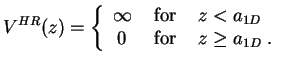 |
(4.17) |
For ![]() , asterisks in Fig. 4.3(c) show the fixed-node diffusion Monte
Carlo (FN-MC) results obtained using the above fictitious hard-rod potential (see
Sec. 4.4.2). Good agreement is found with the exact 1D eigenenergies
obtained from Eqs. 4.11-4.12. For
, asterisks in Fig. 4.3(c) show the fixed-node diffusion Monte
Carlo (FN-MC) results obtained using the above fictitious hard-rod potential (see
Sec. 4.4.2). Good agreement is found with the exact 1D eigenenergies
obtained from Eqs. 4.11-4.12. For ![]() bosons, our 1D FN-MC
algorithm and our usage of the hard-rod equation of state both take advantage of a
reduction of configuration space similar to that discussed here for two bosons (see
Sec. 4.3 and Chapter 2).
bosons, our 1D FN-MC
algorithm and our usage of the hard-rod equation of state both take advantage of a
reduction of configuration space similar to that discussed here for two bosons (see
Sec. 4.3 and Chapter 2).