

Next: Lezione 20 (23 maggio
Up: Matematica Discreta
Previous: Lezione 18 (16 maggio
Subsections
Definizione 19.1
Sia
un grafo, definiamo alcuni grafi costruiti a partire da
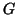
:
- (cancellazione di un lato) se
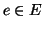 denotiamo
denotiamo
- (aggiunta di un lato) se
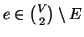 denotiamo
denotiamo
- (cancellazione di un vertice) se
 denotiamo
denotiamo
- (divisione di un lato) se
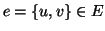 denotiamo
denotiamo
essendo 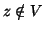 .
.
Esercizio 19.1
Si provi che se
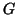
è connesso, allora per ogni
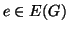
, anche
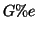
è connesso.
Soluzione
Esercizio 19.2
Si provi che per ogni vertice
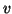
si ha che
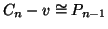
.
Soluzione
Definizione 19.2
Sia
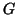
un grafo, diremo che
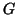
è
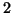
-connseeo se
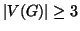
e per
ogni
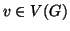
si ha che
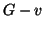
è connesso.
Esercizio 19.3
Si provi che ogni grafo hamiltoniano è
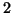
-connesso.
Soluzione
Esercizio 19.4
Si provi che se
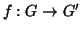
è un isomorfismo, allora per ogni
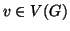
ed
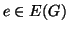
si ha che
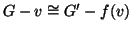
,
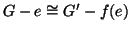
,
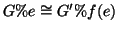
.
Soluzione
Esercizio 19.5
Si provi che se
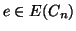
allora
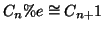
.
Soluzione
Esercizio 19.6
Si provi che se
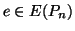
allora
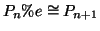
.
Soluzione
Dimostrazione.
Siano 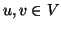 . Dobbiamo provare che esiste una passeggiata tra
. Dobbiamo provare che esiste una passeggiata tra 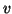 e
e 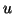 che
non contiene il lato
che
non contiene il lato 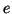 . Si hanno due casi
. Si hanno due casi
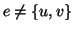 ;
;
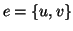 .
.
Nel primo caso, sia 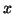 un estremo di
un estremo di 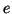 diverso da
diverso da 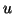 e
e 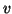 (i.e.
(i.e. 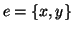 con
con 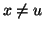 e
e 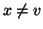 ) allora
) allora 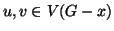 . Dato che
. Dato che 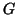 è
è
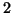 -connesso,
-connesso, 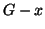 è connesso, e quindi esiste una passeggiata
in
è connesso, e quindi esiste una passeggiata
in 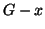 che congiunge
che congiunge 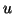 e
e 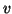 . Dato che
. Dato che 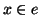 ,
,
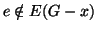 quindi
questa passeggiata non contenere il lato
quindi
questa passeggiata non contenere il lato 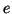 .
.
Nel secondo caso, sia
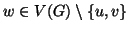 (esiste perché
(esiste perché
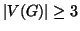 ). Dato che
). Dato che 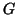 è
è 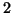 -connesso esiste una passeggiata
-connesso esiste una passeggiata 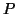 tra
tra 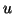 e
e 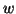 in
in 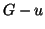 (chiaramente tale passeggiata non passa per
(chiaramente tale passeggiata non passa per 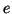 ). Per lo
stesso motivo esiste una passeggiata tra
). Per lo
stesso motivo esiste una passeggiata tra 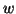 e
e 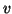 in
in 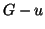 (anche questa
passeggiata non può contenere il lato
(anche questa
passeggiata non può contenere il lato 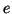 ). Congiungendo queste due
passeggiate si ottiene una passeggiata che congiunge
). Congiungendo queste due
passeggiate si ottiene una passeggiata che congiunge 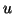 e
e 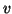 e che non passa
per
e che non passa
per 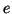 .
.

Osservazione 19.4
Dalla proposizione precedente segue in particolare che ogni grafo
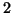
-connesso
è connesso.
Teorema 19.5 (prima caratterizzazione dei grafi
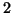
-connessi)
Un grafo
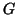
è
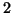
-connesso se e solo se ogni coppia di vertici di
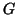
è
contenuta in un ciclo. Ossia
per ogni
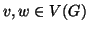
esiste un ciclo
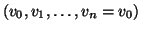
in
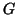
che
passa per i vertci
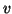
e
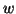
.
Lemma 19.6
Sia
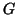
un grafo
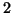
-connesso allora per ogni
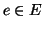
anche
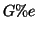
è
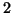
-connesso.
Dimostrazione.
Sia 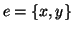 e
e
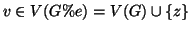 . Si hanno tre casi:
. Si hanno tre casi:
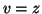 ;
;
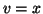 o
o 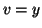 ;
;
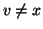 ,
, 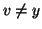 e
e 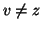
Nel primo caso,
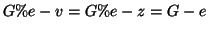 , infatti dalle definizioni si ha
, infatti dalle definizioni si ha
Pertanto 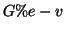 è connesso per la proposizione 19.3
è connesso per la proposizione 19.3
Nel secondo caso, supponiamo che 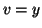 (l'altro caso si ottiene per simmetria,
scambiando
(l'altro caso si ottiene per simmetria,
scambiando 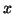 e
e 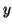 ). Osserviamo che
). Osserviamo che 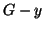 è un sottografo di
è un sottografo di 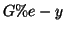 . Infatti
. Infatti
Ma allora dato che ogni 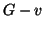 è
è 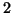 -connesso,
-connesso, 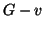 è connesso e quindi ogni
vertice di
è connesso e quindi ogni
vertice di 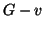 è congiungibile in
è congiungibile in 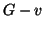 , e quindi in
, e quindi in 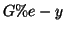 al vertice
al vertice
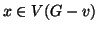 . D'altra parte, l'unico altro vertice di
. D'altra parte, l'unico altro vertice di 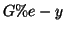 è
è 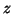 che è
congiungibile a
che è
congiungibile a 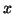 in
in 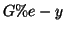 , dato che
, dato che
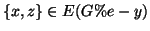 . Tutti i
vertici sono quindi congiungibili tra loro.
. Tutti i
vertici sono quindi congiungibili tra loro.
Nel terzo caso
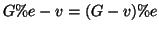 è connesso in quanto ottenuto dal grafo
connesso
è connesso in quanto ottenuto dal grafo
connesso 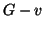 suddividendo un suo lato (
suddividendo un suo lato (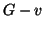 è connesso).
è connesso).

Lemma 19.7
Sia
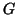
un grafo
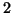
-connesso allora per ogni
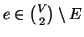
anche
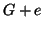
è
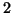
-connesso.
Dimostrazione.
Segue dal fatto che per ogni vertice
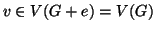 il grafo
il grafo
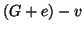 ha gli stessi vertici di
ha gli stessi vertici di 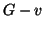 e contiene tutti i lati di
e contiene tutti i lati di 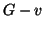 . Dato
che quest'ultimo è connesso, lo ànche
. Dato
che quest'ultimo è connesso, lo ànche 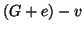 .
.

Teorema 19.8
Un grafo finito
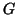
è
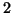
-connesso se e solo se è isomorfo ad un grafo
ottenuto a partire da
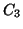
con una successione finita di suddivisioni di ed
aggiunzioni di lati.
Dimostrazione.
Dato che 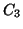 è
è 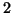 -connesso, i due lemmi precedenti provano che ogni grafo ottenuto da
-connesso, i due lemmi precedenti provano che ogni grafo ottenuto da 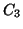 aggiungendo e suddividendo lati è
aggiungendo e suddividendo lati è 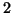 -connesso.
-connesso.
Proviamo l'implicazione opposta. Per semplicità diciamo che un grafo è
costruibile se è ottenuto da 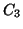 con un numero finito di aggiunzioni
e suddivisioni di nodi. Consideriamo l'insieme
con un numero finito di aggiunzioni
e suddivisioni di nodi. Consideriamo l'insieme
usando l'esercizio 19.5, si prova che ogni ciclo è
costruibile, d'altra parte dal primo teorema di
caratterizzazione segue, in particolare, che 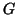 contiene dei cicli. Ma allora
contiene dei cicli. Ma allora
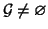 . Sia allora
. Sia allora
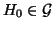 un grafo che massimizza il numero dei
lati (
un grafo che massimizza il numero dei
lati (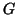 è finito!), ossia tale che
è finito!), ossia tale che
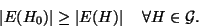 |
(11) |
Proviamo che 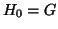 da cui segue evidentemente la tesi.
da cui segue evidentemente la tesi.
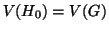 . Supponiamo per assurdo che esista
. Supponiamo per assurdo che esista
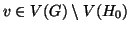 .
.
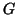 è connesso, esiste quindi un cammino
è connesso, esiste quindi un cammino
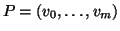 che congiunge
che congiunge 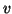 ad un vertice di
ad un vertice di 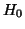 . Sia
. Sia 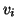 il primo vertice di questo cammino tale che
il primo vertice di questo cammino tale che
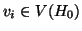 . Chiamiamo
. Chiamiamo 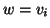 e
e 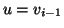 (
(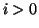 dato che
dato che
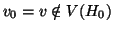 ), allora
), allora
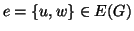 ,
, 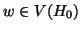 e
e
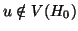 .
.
Il grafo 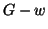 è connesso e, dato che
è connesso e, dato che 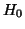 ha almeno tre vertici,
esistono vertici di
ha almeno tre vertici,
esistono vertici di 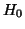 diversi da
diversi da 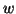 . Sia allora
. Sia allora
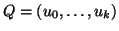 un
cammino in
un
cammino in 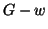 che congiunge
che congiunge 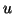 ad un vertice di
ad un vertice di 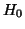 ed i cui altri
vertici sono tutti fuori di
ed i cui altri
vertici sono tutti fuori di 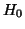 (vedi figura 6), ossia
(vedi figura 6), ossia 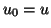 ,
,
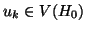 e
e
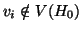 per ogni
per ogni 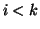 . Consideriamo il grafo
. Consideriamo il grafo 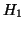 definito da:
definito da:
Figura 6:
Come costruire un cammino che ha solo due punti in comune con 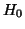
 |
Chiaramente 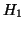 è un sottografo di
è un sottografo di 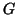 e
e
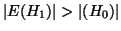 . Se
proviamo che
. Se
proviamo che  è ottenuto da
è ottenuto da 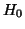 con un numero finito di suddivisioni e
di aggiunzioni di lati si ha che
con un numero finito di suddivisioni e
di aggiunzioni di lati si ha che
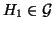 e quindi un assurdo. Ma ora si
hanno due casi:
e quindi un assurdo. Ma ora si
hanno due casi:
-
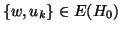
-
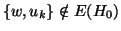
Nel primo caso 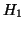 è ottenuto suddividendo
è ottenuto suddividendo 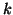 volte il lato
volte il lato 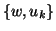 e
quindi aggiungendo di nuovo il lato
e
quindi aggiungendo di nuovo il lato 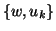 , nel secondo caso
, nel secondo caso 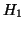 è
ottenuto aggiungendo il lato
è
ottenuto aggiungendo il lato 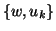 e quindi dividendolo
e quindi dividendolo 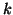 volte (vedi
figura 7).
volte (vedi
figura 7).
Figura 7:
Il grafo 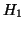 è ottenuto da
è ottenuto da 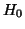 o aggiungendo un lato e quindi
suddividendolo oppure suddividendo un lato già esistente e quindi
riaggiungendolo.
o aggiungendo un lato e quindi
suddividendolo oppure suddividendo un lato già esistente e quindi
riaggiungendolo.
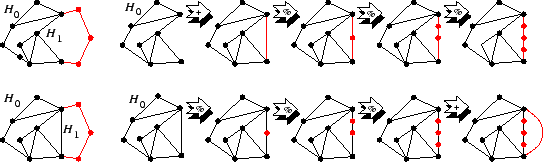 |
 . Supponiamo per assurdo che
. Supponiamo per assurdo che
 , allora,
visto che per il punto precedente
, allora,
visto che per il punto precedente 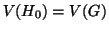 , necessariamente
, necessariamente
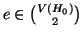 , si può allora costruire il grafo
, si può allora costruire il grafo 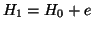 che
è un sottografo di
che
è un sottografo di 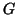 . D'altra parte
. D'altra parte 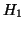 è ottenuto da
è ottenuto da 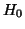 aggiungendo
un lato, quindi è costruibile, ovvero
aggiungendo
un lato, quindi è costruibile, ovvero
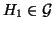 . Ma
. Ma
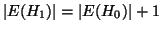 , che contraddice la (11).
, che contraddice la (11).

Esercizio 19.7
Siano
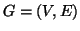
e
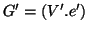
due grafi. Si denoti con
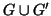
il grafo
tale che
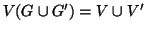
e
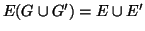
. Si provi che se
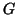
e
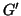
sono connessi e
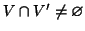
allora
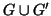
è connesso.
Soluzione
Esercizio 19.8
Si provi che se
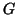
e
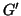
sono 2-connessi e
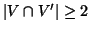
allora
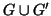
è 2-connesso.
Soluzione
Esercizio 19.9
Sia
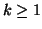
, si dice che un grafo
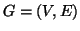
è
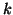 -connesso
-connesso se per ogni
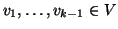
si ha che
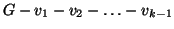
è connesso. Si
osservi che
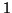
-connesso è sinonimo di connesso.
Si provi che 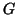 è
è 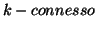 se e solo se per ogni
se e solo se per ogni 
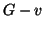 è
è
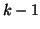 -connesso.
-connesso.
Soluzione
Esercizio 19.10
Si determinino condizioni sufficienti affinché l'unione di due grafi
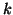
-connessi sia ancora
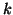
-connesso.
Soluzione
Esercizio 19.11
Per ogni
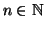
sia
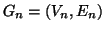
un grafo connesso e si supponga che
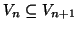
per ogni
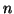
. Si provi che allora
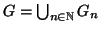
è connesso.
Soluzione
Esercizio 19.12
Per ogni
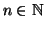
sia
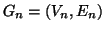
un grafo connesso e si supponga che
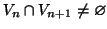
per ogni
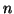
. Si provi che allora
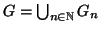
è connesso.
Soluzione
Esercizio 19.13
Per ogni
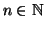
sia
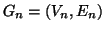
un grafo
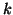
-connesso e si supponga che
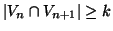
per ogni
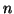
. Si provi che allora
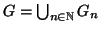
è
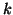
-connesso.
Soluzione


Next: Lezione 20 (23 maggio
Up: Matematica Discreta
Previous: Lezione 18 (16 maggio
Luminati Domenico
2002-06-07
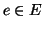 denotiamo
denotiamo
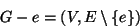
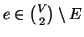 denotiamo
denotiamo
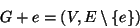
 denotiamo
denotiamo
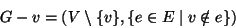
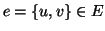 denotiamo
denotiamo
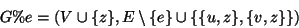
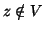 .
.
![]() . Dobbiamo provare che esiste una passeggiata tra
. Dobbiamo provare che esiste una passeggiata tra ![]() e
e ![]() che
non contiene il lato
che
non contiene il lato ![]() . Si hanno due casi
. Si hanno due casi
![]() (esiste perché
(esiste perché
![]() ). Dato che
). Dato che ![]() è
è ![]() -connesso esiste una passeggiata
-connesso esiste una passeggiata ![]() tra
tra ![]() e
e ![]() in
in ![]() (chiaramente tale passeggiata non passa per
(chiaramente tale passeggiata non passa per ![]() ). Per lo
stesso motivo esiste una passeggiata tra
). Per lo
stesso motivo esiste una passeggiata tra ![]() e
e ![]() in
in ![]() (anche questa
passeggiata non può contenere il lato
(anche questa
passeggiata non può contenere il lato ![]() ). Congiungendo queste due
passeggiate si ottiene una passeggiata che congiunge
). Congiungendo queste due
passeggiate si ottiene una passeggiata che congiunge ![]() e
e ![]() e che non passa
per
e che non passa
per ![]() .
.
![]()
![]() e
e
![]() . Si hanno tre casi:
. Si hanno tre casi:
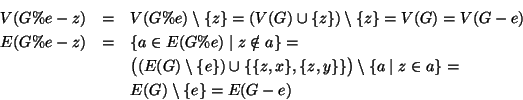
![]() (l'altro caso si ottiene per simmetria,
scambiando
(l'altro caso si ottiene per simmetria,
scambiando ![]() e
e ![]() ). Osserviamo che
). Osserviamo che ![]() è un sottografo di
è un sottografo di ![]() . Infatti
. Infatti
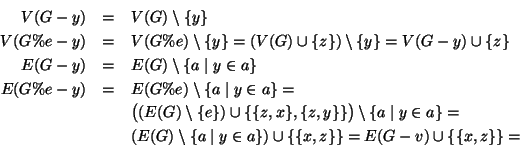
![]() è connesso in quanto ottenuto dal grafo
connesso
è connesso in quanto ottenuto dal grafo
connesso ![]() suddividendo un suo lato (
suddividendo un suo lato (![]() è connesso).
è connesso).
![]()
![]() il grafo
il grafo
![]() ha gli stessi vertici di
ha gli stessi vertici di ![]() e contiene tutti i lati di
e contiene tutti i lati di ![]() . Dato
che quest'ultimo è connesso, lo ànche
. Dato
che quest'ultimo è connesso, lo ànche ![]() .
.
![]()
![]() è
è ![]() -connesso, i due lemmi precedenti provano che ogni grafo ottenuto da
-connesso, i due lemmi precedenti provano che ogni grafo ottenuto da ![]() aggiungendo e suddividendo lati è
aggiungendo e suddividendo lati è ![]() -connesso.
-connesso.
![]() con un numero finito di aggiunzioni
e suddivisioni di nodi. Consideriamo l'insieme
con un numero finito di aggiunzioni
e suddivisioni di nodi. Consideriamo l'insieme
![]() . Supponiamo per assurdo che esista
. Supponiamo per assurdo che esista
![]() .
.
![]() è connesso, esiste quindi un cammino
è connesso, esiste quindi un cammino
![]() che congiunge
che congiunge ![]() ad un vertice di
ad un vertice di ![]() . Sia
. Sia ![]() il primo vertice di questo cammino tale che
il primo vertice di questo cammino tale che
![]() . Chiamiamo
. Chiamiamo ![]() e
e ![]() (
(![]() dato che
dato che
![]() ), allora
), allora
![]() ,
, ![]() e
e
![]() .
.
![]() è connesso e, dato che
è connesso e, dato che ![]() ha almeno tre vertici,
esistono vertici di
ha almeno tre vertici,
esistono vertici di ![]() diversi da
diversi da ![]() . Sia allora
. Sia allora
![]() un
cammino in
un
cammino in ![]() che congiunge
che congiunge ![]() ad un vertice di
ad un vertice di ![]() ed i cui altri
vertici sono tutti fuori di
ed i cui altri
vertici sono tutti fuori di ![]() (vedi figura 6), ossia
(vedi figura 6), ossia ![]() ,
,
![]() e
e
![]() per ogni
per ogni ![]() . Consideriamo il grafo
. Consideriamo il grafo ![]() definito da:
definito da:
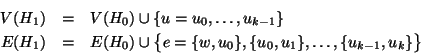

![]() è
è ![]() se e solo se per ogni
se e solo se per ogni ![]()
![]() è
è
![]() -connesso.
-connesso.