

Next: Lezione 17 (14 maggio
Up: Matematica Discreta
Previous: Lezione 15 (7 maggio
Subsections
Definizione 16.1
Sia
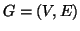
un grafo e siano
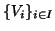
le classi d'equivalenza di
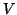
rispetto alla relazione di congiungibilità. I grafi
![$G[V_i]$](img1303.gif)
, indotti da
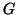
sui
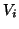
, vengono detti le
componenti connesse di
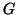
.
Proposizione 16.2
Sia
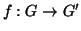
un morfismo di grafi e
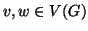
.
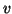
e
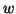
sono
congiungibili allora anche
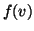
e
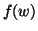
lo sono.
Dimostrazione.
Se
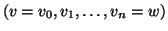 è una passeggiata, allora, per
definizione di morfismo, anche
è una passeggiata, allora, per
definizione di morfismo, anche
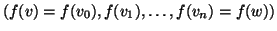 lo è.
lo è.

Proposizione 16.3
Sia
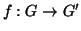
un isomorfismo di grafi e
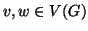
.
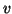
e
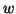
sono
congiungibili se e solo se lo sono
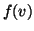
e
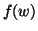
.
Dimostrazione.
Segue immediatamente dalla proposizione precedente applicata ad 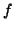 e ad
e ad
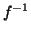 .
.

Teorema 16.4
Siano
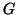
e
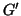
grafi isomorfi, allora hanno componenti connesse isomorfe.
Più precisamente, se
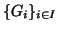
e
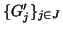
sono gli
insiemi delle componenti connesse di
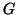
e
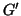
rispettivamente, allora
esiste una bigezione
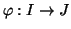
tale che

.
Dimostrazione.
Siano
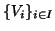 le classi d'equivalenza di
le classi d'equivalenza di 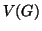 (rispetto alla
congiungibilità
(rispetto alla
congiungibilità 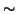 ) e
) e
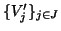 quelle di
quelle di 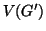 .
.
Proviamo innanzitutto che per ogni 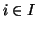 esiste un unico
esiste un unico 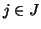 tale che
tale che
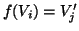 . Infatti sia
. Infatti sia  , dato che
, dato che
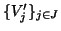 è una
partizione di
è una
partizione di 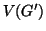 , si ha che esiste un unico
, si ha che esiste un unico 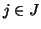 tale che
tale che 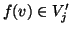 . Ma ora
. Ma ora 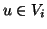 se e solo se
se e solo se 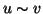 (per definizione di
classe d'equivalenza) e dato che
(per definizione di
classe d'equivalenza) e dato che 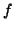 è un isomorfismo, per la proposizione
precedente, questo equivale a dire che
è un isomorfismo, per la proposizione
precedente, questo equivale a dire che
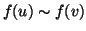 ovvero che
ovvero che 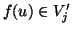 , ovvero
, ovvero
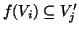 . D'altra parte se
. D'altra parte se 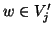 allora
allora 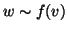 , quindi, dato che
, quindi, dato che 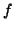 è un isomorfismo
è un isomorfismo
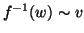 e quindi
e quindi
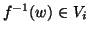 . Questo prova quindi che
. Questo prova quindi che 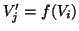 .
.
Per ogni 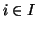 , indichiamo con
, indichiamo con 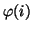 l'unico
l'unico 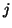 con la proprietà
precedente.
con la proprietà
precedente.
Proviamo che per ogni 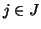 esiste un unico
esiste un unico 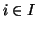 tale che
tale che 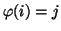 ,
ossia
,
ossia
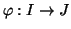 è bigettiva. Dato
è bigettiva. Dato 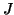 , sia
, sia 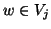 , dato che
, dato che 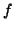 è
bigettiva, esiste un unico
è
bigettiva, esiste un unico 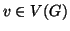 tale che
tale che 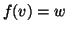 . Esiste allora un unico
. Esiste allora un unico
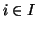 tale che
tale che  , e questo è quindi l'unico tale che
, e questo è quindi l'unico tale che 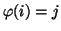 .
.
Per concludere proviamo che 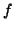 induce un isomorfismo tra
induce un isomorfismo tra ![$G[V_i]$](img1303.gif) e
e
![$G'[V'_\varphi (i)]$](img1333.gif) . Ma chiaramente, dato che
. Ma chiaramente, dato che 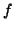 è bigettiva e
è bigettiva e
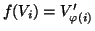 , anche
, anche
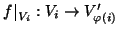 è
bigettiva. Inoltre, se
è
bigettiva. Inoltre, se 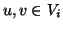 , per definizione di sottografo
indotto,
, per definizione di sottografo
indotto,
![$\{u,v\}\in
E(G[V_i])$](img1337.gif) se e solo se
se e solo se
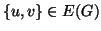 e questo, per la proprietà di
isomorfism di
e questo, per la proprietà di
isomorfism di 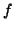 equivale a dire che
equivale a dire che
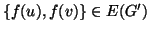 e dato che
e dato che
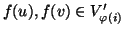 , questo è a sua volta equivalente a dire che
, questo è a sua volta equivalente a dire che
![$\{f(u),f(v)\}\in E(G'[V'_{\varphi (i)}])$](img1341.gif) . E questa è la tesi.
. E questa è la tesi.

Esercizio 16.1
Si provi che se
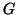
è un grafo e
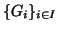
sono le sue componenti
connesse, allora
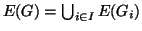
.
Soluzione
Esercizio 16.2
Se
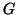
è un grafo finito e
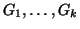
sono le sue componenti connesse,
allora
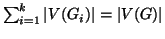
e
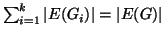
.
Soluzione
Definizione 16.5
Un grafo si dice connesso se ha una sola componente connessa. Un grafo
non connesso si dice sconnesso.
Osservazione 16.6
Un grafo
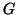
è connesso se e solo se per ogni
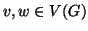
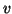
e
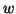
sono
congiungibili da un cammino (risp. da una passeggiata).
Osservazione 16.7
Dal teorema
16.4 segue in particolare che se due grafi sono
isomorfi, allora o sono entrambi connessi oppure sono entrambi sconnessi.
Esercizio 16.3
Si provi che se
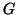
è un grafo e
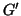
è un sottografo di
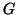
connesso e
che contiene tutti i vertici (i.e.
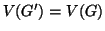
), allora anche
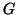
è
connesso.
Soluzione
Definizione 16.8
Sia
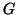
un grafo finito e siano
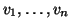
i sui vertici. Si chiama
matrice di incidenza di
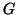
la matrice
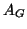
, che al posto
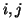
ha
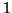
se
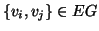
e ha
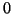
altrimenti.
Proposizione 16.9
Sia
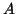
la matrice di incidenza del grafo
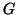
, allora l'elemeto di posto
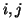
della matrice
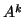
è pari al numero di passeggiate lunghe
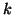
dal
vertice
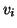
al vertice
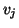
.
Esercizio 16.4
Si provi che un grafo finito
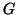
ha
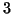
-cicli se e solo se la matrice
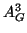
ha elementi non nulli sulla diagonale.
Soluzione
Esercizio 16.5
Si provi che il numero di
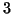
-cicli di un grafo finito
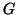
è pari a
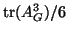
.
Soluzione


Next: Lezione 17 (14 maggio
Up: Matematica Discreta
Previous: Lezione 15 (7 maggio
Luminati Domenico
2002-06-07
![]() è una passeggiata, allora, per
definizione di morfismo, anche
è una passeggiata, allora, per
definizione di morfismo, anche
![]() lo è.
lo è.
![]()
![]() e ad
e ad
![]() .
.
![]()
![]() le classi d'equivalenza di
le classi d'equivalenza di ![]() (rispetto alla
congiungibilità
(rispetto alla
congiungibilità ![]() ) e
) e
![]() quelle di
quelle di ![]() .
.
![]() esiste un unico
esiste un unico ![]() tale che
tale che
![]() . Infatti sia
. Infatti sia ![]() , dato che
, dato che
![]() è una
partizione di
è una
partizione di ![]() , si ha che esiste un unico
, si ha che esiste un unico ![]() tale che
tale che ![]() . Ma ora
. Ma ora ![]() se e solo se
se e solo se ![]() (per definizione di
classe d'equivalenza) e dato che
(per definizione di
classe d'equivalenza) e dato che ![]() è un isomorfismo, per la proposizione
precedente, questo equivale a dire che
è un isomorfismo, per la proposizione
precedente, questo equivale a dire che
![]() ovvero che
ovvero che ![]() , ovvero
, ovvero
![]() . D'altra parte se
. D'altra parte se ![]() allora
allora ![]() , quindi, dato che
, quindi, dato che ![]() è un isomorfismo
è un isomorfismo
![]() e quindi
e quindi
![]() . Questo prova quindi che
. Questo prova quindi che ![]() .
.
![]() , indichiamo con
, indichiamo con ![]() l'unico
l'unico ![]() con la proprietà
precedente.
con la proprietà
precedente.
![]() esiste un unico
esiste un unico ![]() tale che
tale che ![]() ,
ossia
,
ossia
![]() è bigettiva. Dato
è bigettiva. Dato ![]() , sia
, sia ![]() , dato che
, dato che ![]() è
bigettiva, esiste un unico
è
bigettiva, esiste un unico ![]() tale che
tale che ![]() . Esiste allora un unico
. Esiste allora un unico
![]() tale che
tale che ![]() , e questo è quindi l'unico tale che
, e questo è quindi l'unico tale che ![]() .
.
![]() induce un isomorfismo tra
induce un isomorfismo tra ![]() e
e
![]() . Ma chiaramente, dato che
. Ma chiaramente, dato che ![]() è bigettiva e
è bigettiva e
![]() , anche
, anche
![]() è
bigettiva. Inoltre, se
è
bigettiva. Inoltre, se ![]() , per definizione di sottografo
indotto,
, per definizione di sottografo
indotto,
![]() se e solo se
se e solo se
![]() e questo, per la proprietà di
isomorfism di
e questo, per la proprietà di
isomorfism di ![]() equivale a dire che
equivale a dire che
![]() e dato che
e dato che
![]() , questo è a sua volta equivalente a dire che
, questo è a sua volta equivalente a dire che
![]() . E questa è la tesi.
. E questa è la tesi.
![]()