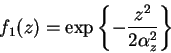 |
(2.64) |
In the case of the Hamiltonian (4.9) we use Gaussian construction for the
one-body Bijl-Jastrow term
The cut-off length ![]() is fixed at
is fixed at
![]() , while the wave vector
, while the wave vector
![]() is chosen such that the boundary condition at
is chosen such that the boundary condition at ![]() imposed by the
imposed by the
![]() -function potential is satisfied:
-function potential is satisfied:
![]() . For
negative
. For
negative ![]() (
(![]() ) the correlation function, Eq. 2.65, is
positive everywhere. For positive
) the correlation function, Eq. 2.65, is
positive everywhere. For positive ![]() (
(![]() ), in contrast,
), in contrast, ![]() changes sign at
changes sign at ![]() . The parameterization given by Eq. 2.65 is used
in our stability analysis performed within a VMC framework (see Sec. 4.5)
and in our DMC calculations for
. The parameterization given by Eq. 2.65 is used
in our stability analysis performed within a VMC framework (see Sec. 4.5)
and in our DMC calculations for ![]() . To perform the FN-DMC calculations for
negative
. To perform the FN-DMC calculations for
negative ![]() , we need to construct a trial wave function that is positive
definite everywhere. In the FN-DMC calculations, we thus use an alternative
parameterization, which imposes the constraint
, we need to construct a trial wave function that is positive
definite everywhere. In the FN-DMC calculations, we thus use an alternative
parameterization, which imposes the constraint ![]() for
for ![]() ,
,