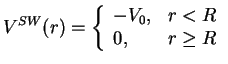 |
(1.89) |
Let us consider an attractive version of the soft sphere potential (1.52):
Interaction (1.89) is called a square-well potential, with ![]() (positive) being its depth and
(positive) being its depth and ![]() being its range. The Schrödinger equation
(1.41) for a pair of particles in the center of mass system is given by
being its range. The Schrödinger equation
(1.41) for a pair of particles in the center of mass system is given by
We are interested in finding solutions with positive energies, as that are the
solutions corresponding to a scattered state, instead solutions with negative energy
are localized. On the opposite to the situation described in Sec. 1.3.5.1, the
interaction potential is always lower than the value of the scattering energy
![]() . For convenience we introduce
. For convenience we introduce
![]() . In both regions
the solution is a free-wave like:
. In both regions
the solution is a free-wave like:
The condition (1.40) immediately fixes the phase ![]() . The matching
equations for the function and its derivative read as
. The matching
equations for the function and its derivative read as
Condition of the continuity of the logarithmic derivative
![]() fixes the phase
fixes the phase ![]() of the solution
of the solution
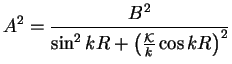 |
(1.95) |
By taking limit of low energy in (1.94) and using the definition
(1.44) one obtains the expression for the ![]() -wave scattering length:
-wave scattering length:
The dependence of the scattering length of the scattering on a soft sphere potential
(Eq. 1.59) looks similar to (1.96) with the only difference that the
trigonometric tangent is substituted with the hyperbolic one. The difference is
crucial. Indeed, as
![]() , the scattering length on the SS potential is
always smaller than the range of the potential. Instead, the term
, the scattering length on the SS potential is
always smaller than the range of the potential. Instead, the term
![]() is
unbound. When the scattering happens at resonant momentum
is
unbound. When the scattering happens at resonant momentum
![]() with small detuning
with small detuning
![]() , the scattering
length becomes extremely large and changes its sign.
, the scattering
length becomes extremely large and changes its sign.
The square well potential is attractive and in principle can have the bound state
solution with energy
![]() . In outer region
. In outer region ![]() the solution
(1.92) gets modified and decays exponentially fast. The condition of the
continuity of the logarithmic derivative in the limit
the solution
(1.92) gets modified and decays exponentially fast. The condition of the
continuity of the logarithmic derivative in the limit ![]() is
is
![]() . This condition can not be satisfied before crossing the resonance,
as inequality
. This condition can not be satisfied before crossing the resonance,
as inequality
![]() holds for arguments
holds for arguments ![]() . Instead immediately
after the resonance position
. Instead immediately
after the resonance position
![]() a shallow bound state appears in the
system.
a shallow bound state appears in the
system.