The wave function of the perturbation, ![]() , was obtained in the momentum
representation and is given by expression (7.5). The spatial dependence,
, was obtained in the momentum
representation and is given by expression (7.5). The spatial dependence,
![]() , is related to
, is related to ![]() by means of the Fourier
transformation. We will find the density profile
by means of the Fourier
transformation. We will find the density profile
![]() . Within the
same level of accuracy, as in the calculations above,
. Within the
same level of accuracy, as in the calculations above, ![]() is given by
is given by
| (7.43) |
In terms of Fourier components one has
![]()
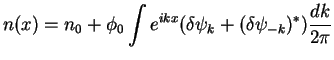 |
(7.44) |
There are two cases to be considered separately:
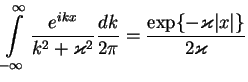 |
(7.46) |
Thus, the density perturbation has a form of a bump and decays exponentially fast:
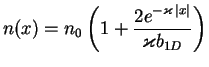 |
(7.47) |
For a repulsive interaction with the impurity the scattering length is negative
![]() and the density is suppressed by the presence of the impurity. Instead an
attractive interaction
and the density is suppressed by the presence of the impurity. Instead an
attractive interaction ![]() leads to an increase in the density.
leads to an increase in the density.
In this case for ![]() the pole is absent and the integral vanishes. This means that
there is no perturbation in front of the impurity (impurity moves to the right).
the pole is absent and the integral vanishes. This means that
there is no perturbation in front of the impurity (impurity moves to the right).
Instead for ![]() the pole is present and the integral is different from zero.
the pole is present and the integral is different from zero.
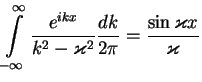 |
(7.48) |
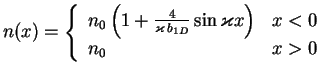 |
(7.49) |
The condition of the applicability of the perturbation theory demands the
perturbation ![]() be small compared to the unperturbed solution
be small compared to the unperturbed solution ![]() . This
condition is satisfied if the velocity of the impurity
. This
condition is satisfied if the velocity of the impurity ![]() is not to close to the
speed of sound
is not to close to the
speed of sound ![]() .
.