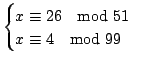
Il sistema è equivalente a
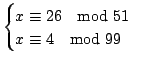
Soluzione dell'esercizio 2 Sia ![]() . Un grafo
. Un grafo ![]() ammette come albero di copertura
ammette come albero di copertura ![]() se e solo
se ha come insieme di vertici
se e solo
se ha come insieme di vertici ![]() (i.e.
(i.e. ![]() ) e se ha
) e se ha ![]() come
sottografo ossia se e solo se
come
sottografo ossia se e solo se
![]() . Ma allora l'insieme
dei grafi richiesto è in bigezione con l'insieme
. Ma allora l'insieme
dei grafi richiesto è in bigezione con l'insieme
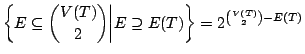
Dato che
![]() allora
allora
![]() e quindi la
cardinalità cercata è pari a
e quindi la
cardinalità cercata è pari a
Soluzione dell'esercizio 3 Se ![]() è un grafo tale che
è un grafo tale che
![]() allora
allora
![]() e ci sono tre vertci di grado
e ci sono tre vertci di grado ![]() . Ma allora ogni altro vertice deve
essere adiacente a questi tre, e quindi ogni altro vertice dovrebbe
avere grado almeno
. Ma allora ogni altro vertice deve
essere adiacente a questi tre, e quindi ogni altro vertice dovrebbe
avere grado almeno ![]() , mentre in
, mentre in ![]() ci sono due
ci sono due ![]() .
.
Per ![]() usiamo il teorema dello score:
usiamo il teorema dello score:
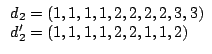
(1). La risposta è sì. Si prenda ad esempio l'albero in figura 1.
(2). La risposta è sì. Basta prendere il grafo in figura 2 .
(3). La risposta è no. Un grafo ![]() -connesso non
può avere vertici di grado
-connesso non
può avere vertici di grado ![]() , mentre ogni grafo che realizza
, mentre ogni grafo che realizza ![]() ne ha
ne ha ![]() .
.
![]()
Soluzione dell'esercizio 4
![]() è l'insieme degli elementi invertibili di
è l'insieme degli elementi invertibili di
![]() e
quindi
e
quindi
![]() .
(1). Osserviamo che
.
(1). Osserviamo che ![]() ,
,
![]() ,
,
![]() , quindi i lati di
, quindi i lati di ![]() sono dati da
sono dati da
Invece ![]() e quindi i lati sono dati da
e quindi i lati sono dati da
(2). Per quanto osservato sopra, basta trovare tutti gli
![]() tali che
tali che ![]() e
e ![]() . Si vede facilmente che questo
insieme è
. Si vede facilmente che questo
insieme è
![]() .
.
(3).
Un tale ![]() esiste, basta prendere
esiste, basta prendere ![]() . In questo caso infatti il
grafo non ha lati e quindi non è isomorfo né a
. In questo caso infatti il
grafo non ha lati e quindi non è isomorfo né a ![]() né a
né a ![]() .
.
![]()