Next: About this document ... Up: Matematica Discreta (II modulo) Previous: Matematica Discreta (II modulo)

Soluzioni proposte

Soluzione dell'esercizio 1 $(117,81)=9\mathrel{\big\vert}-9 = 11-20$ quindi il sistema e` risolubile. Inoltre $9 = (-2) \cdot 117 + (3) \cdot 81$ quindi $11-20= -9 \cdot -1 = (9) \cdot 2 + (117) \cdot -3$ quindi

è una soluzione del sistema. Tutte le soluzioni sono allora date da $\{ 254 + k [254,117] \mid k\in\mathbb{Z}\}=\{ 81 + k 254 \mid k\in\mathbb{Z}\}$ .

Soluzione dell'esercizio 2 (1). $\left\vert A\right\vert=\Phi(18)=6$ , $\left\vert B\right\vert=15$ . Ma allora $\mathcal{F}_2=\varnothing$ e quindi $\left\vert\mathcal{F}_2\right\vert=0$ . Invece $\left\vert\mathcal{F}_1\right\vert=\frac{15!}{(15-6)!}=\frac{15!}{9!}=3603600$ .

(2). Indichiamo con l'insieme delle permutazioni di e con $S_{A \setminus C}$ l'insieme delle permutazioni di $A\setminus C$ . Allora la funzione

$\displaystyle \Psi$	$\displaystyle :$	$\displaystyle S_{A \setminus C} \times S_{C} \to \mathcal{F}_3$
$\displaystyle \Psi$	$\displaystyle :$	$\displaystyle (f,\sigma) \mapsto f \cup \sigma$

è una bigezione, la cui inversa è data da:

$\displaystyle \Psi^{-1}$	$\displaystyle :$	$\displaystyle \mathcal{F}_3 \to S_{A \setminus C} \times S_{C}$
$\displaystyle \Psi^{-1}$	$\displaystyle :$	$\displaystyle f \mapsto (\setbox\restrictbox=\hbox{$\hbox{$f$}_{A \setminus C}$... ...ctbox depth\dp\restrictbox\, \hbox{\vrule depth\dp0 height \ht0 width0pt}_{C}})$

Ma allora $\left\vert\mathcal{F}_3\right\vert= \left\vert S_{A \setminus C} \times S_{C}\... ...\vert A \setminus C\right\vert! \cdot \left\vert C\right\vert! = 4!\cdot 2! =48$

(3). Affinché una funzione $A \to \{1,2\}$ non sia suriettiva è necessario e sufficiente che sia non costante. D'altra parte le funzioni $A\to \{0,1\}$ non costanti sono esattamente e quindi $\left\vert\mathcal{F}_4\right\vert= 2^{\left\vert A\right\vert}-2=2^6-2=62$ .

Soluzione dell'esercizio 3 (1). Sia il numero di vertici di grado e il numero di vertici di grado . Dato che ci sono soltanto vertici di grado , e , e quelli di grado sono , si ha che $\left\vert V(T)\right\vert= n + k + 5$ . Ma allora, dato che è un albero

$\displaystyle \left\vert E(T)\right\vert = \left\vert V(T)\right\vert-1 = n+k+4.$

D'altra parte

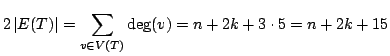
$\displaystyle 2\left\vert E(T)\right\vert = \sum_{v\in V(T)} \deg (v) = n + 2k + 3\cdot 5 = n+2k+15$

Dalle due relazioni si ottiene allora

$\displaystyle 2n +2k+8 = n+2k+15$

da cui

(2). I due alberi in figura 1 hanno la proprietà richiesta (esattamente 5 vertici di grado ) ma non sono isomorfi, dato che hanno un numero diverso di vertici

**Figura 1:** Duae alberi non isomorfi e con le proprietà richieste nell'esercizio 3
$\begin{figure}\centering \psfig{file=fig_a2_1_e32_2003.eps,width=.8\hsize} \end{figure}$

(3). Se è un albero con la proprietà suddetta, e è una sua foglia, allora se $w\not\in V(T)$ si consideri l'albero $T'=(V(T)\cup\{w\}, E(T)\cup \{\{v,w\}\})$ . Chiaramente ha ancora la stessa proprietà, ma ha un vertice in più. Con questa tecnica si possono allora costruire una infinità di alberi a dua a due non isomorfi, in quanto aventi un diverso numero di vertici, ma tutti con esattamente vertici di grado .