


Next: Calcolo combinatorio
Up: Esercizi
Previous: Esercizi
Esercizio 1.1
Si dimostri che:
Con
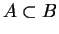
si intende
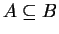
ma
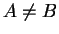
.
Esercizio 1.2
Si dimostri che
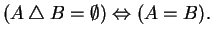
Esercizio 1.3
Siano
A e
B due insiemi e sia
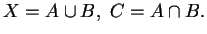
Supponiamo che gli insiemi
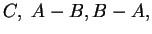
siano non vuoti.
Quali delle seguenti affermazioni è vera?
Esercizio 1.4
Descrivere l'insieme dato dalla differenza simmetrica dei seguenti insiemi:
,
.
Esercizio 1.5
Sia
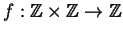
definita da
f(m,n)=mn +m+n.
È vero che
f è iniettiva?
È vero che
f è suriettiva?
Trovare
f-1(4).
Esercizio 1.6
Sia
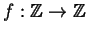
l'applicazione definita da
f(
n) =4
n +1. Dire se
f è iniettiva e/o suriettiva. Trovare
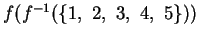
.
Esiste
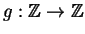
tale che
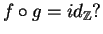
Esercizio 1.7
Sia
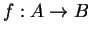
un'applicazione e
X e
Y sottinsiemi di
A,
mostrare che
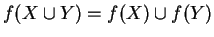
e che
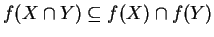
.
Si mostri che se
f è iniettiva si ha che
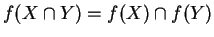
.
Esercizio 1.8
Dati
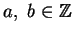
si consideri l'applicazione
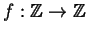
definita da
f(
x) =
ax +
b; si determini per quali valori di
a e
b l'applicazione è biiettiva.
Esercizio 1.9
Sia
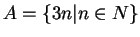
un sottinsieme di
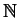
.
Dimostrare che
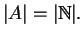
Dimostrare che il complementare di
A in
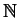
è equipotente a
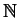
.
Esercizio 1.10
Si consideri l'insieme
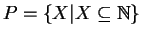
,
mostrare che
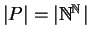
.
Esercizio 1.11
Mostrare che gli intervalli
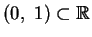
e
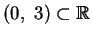
sono equipotenti.
Esercizio 1.12
Siano
X e
Y insiemi finiti e siano
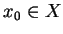
e
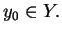
Si determini in funzione delle cardinalità di
X e
Y la cardinalità dei seguenti insiemi:
,
Esercizio 1.13
Siano
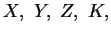
insiemi finiti a due a due disgiunti, calcolare
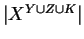
.
Esercizio 1.14
Sia
A un insieme e sia
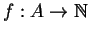
un'applicazione iniettiva, si risponda ai seguenti quesiti:
- 1.
- Sapendo che
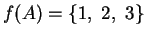 cosa posso dire della cardinalità di A?
cosa posso dire della cardinalità di A?
- 2.
- Sapendo che f(A) è un sottinsieme proprio di
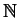 ,
cosa posso dire della cardinalità di A?
,
cosa posso dire della cardinalità di A?
Esercizio 1.15
Si consideri l'insieme
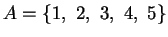
.
Determinare il numero dei sottinsiemi di
A.
Sia
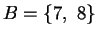
,
determinare la cardinalità di
AB e di
BA.
Sia
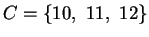
,
determinare
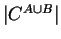
.



Next: Calcolo combinatorio
Up: Esercizi
Previous: Esercizi
Domenico Luminati
2001-05-21