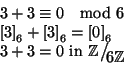Dimostrazione.
1.
![]() per ogni
per ogni
![]() .
.
2. Se
![]() allora a-b=kn e quindi
b-a=(-k)n e quindi
allora a-b=kn e quindi
b-a=(-k)n e quindi
![]() ossia
ossia
![]() .
.
3. Se
![]() e
e
![]() allora
a-b=kn e b-c=hn e quindi
a-c=a-b+b-c=kn+hn=(k+h)n e quindi
allora
a-b=kn e b-c=hn e quindi
a-c=a-b+b-c=kn+hn=(k+h)n e quindi
![]() .
.
![]()
Ricordiamo la definizione di relazione d'equivalenza su un insieme.
L'isieme costituito da tutte le classi d'equivalenza si chiama insieme
quoziente di X modulo ![]() e si denota con il simbolo
e si denota con il simbolo
![]() ,
quindi:
,
quindi:
Dimostrazione. 1. Segue dalla proprietà riflessiva.
2. Se
![]() in particolare
in particolare
![]() e quindi
e quindi ![]() .
Viceversa sia
.
Viceversa sia
![]() .
Se
.
Se
![]() allora
allora ![]() ;
per la
proprietà transitiva
;
per la
proprietà transitiva ![]() ossia
ossia
![]() ,
ossia
,
ossia
![]() .
Scambiando i ruoli di x e y si ha
anche l'inclusione opposta e quindi l'uguaglianza.
.
Scambiando i ruoli di x e y si ha
anche l'inclusione opposta e quindi l'uguaglianza.
3. Se
![]() allora
allora
![]() e
e ![]() ,
usando le proprietà
simmetrica e transitiva si ha
allora che
,
usando le proprietà
simmetrica e transitiva si ha
allora che ![]() e quindi, per la (2), appena
dimostrata,
e quindi, per la (2), appena
dimostrata,
![]() .
.
![]()
In virtù di questa osservazione e della proposizione 11.8 si ha la seguente:
Dimostrazione.
a=nq+r quindi
![]() .
.
![]()
Dimostrazione.
Da 11.13 e dalla 2 di
11.12 segue immediatamente che l'insieme in questione
ha al più n elementi e precisamente
![]() .
D'altra parte se
.
D'altra parte se
![]() allora 0<k-h<n e quindi
allora 0<k-h<n e quindi
![]() e quindi (sempre
per la 2 di 11.12)
e quindi (sempre
per la 2 di 11.12)
![]() .
.
![]()
Dimostrazione.
(1). Se
![]() e
e
![]() allora
allora
![]() .
.
(2). Esistono
![]() tali che a=a'+kn e b=b'+hn, ma
allora, moltiplicando membro a membro si ottiene
ab=a'b'+a'hn+b'kn+hkn2=a'b'+n(a'h+b'k+hkn) e quindi la tesi.
tali che a=a'+kn e b=b'+hn, ma
allora, moltiplicando membro a membro si ottiene
ab=a'b'+a'hn+b'kn+hkn2=a'b'+n(a'h+b'k+hkn) e quindi la tesi.
![]()
![\begin{eqnarray*}\left[a\right]_n+\left[b\right]_n & = & \left[a+b\right]_n
\\
\left[a\right]_n \left[b\right]_n & = & \left[ab\right]_n
\end{eqnarray*}](img684.gif)
Nel seguito, quando parleremo di classi di congruenza e di operazioni tra esse,
potrà succedere che, nella notazione, confonderemo la classe con uno dei suoi
rappresentanti. Sarà chiaro dal contesto a cosa ci si starà riferendo. Ad
esempio useremo indifferentemente una delle tre espressioni