


Next: Lezione 2 (28 febbraio
Up: Matematica Discreta (II modulo)
Previous: Matematica Discreta (II modulo)
Subsections
Insiemi e operazioni tra insiemi
Non intendiamo qui dare un'assiomatica della teoria degli insiemi (cosa che
esula dalle finalità di questo corso e demandata ad altri eventuali corsi
successivi), ma soltanto elencare alcune delle proprietà e delle costruzioni
che permettono di confrontare insiemi e costruire nuovi insiemi a partire da
altri, facendo eventualmente notare la necessità di assiomatizzare tali
cosatruzioni.
Per noi un insieme sarà soltanto una collezione di oggetti detti i suoi elementi. La proprietà fondamentale che si richiede affinché un oggetto
sia un insieme è che si possa sempre stabilire senza ambiguità se qualche
cosa è un suo elemento oppure no. In simboli, se A è un insieme allora per
ogni x si ha che 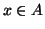 (x appartiene ad A) oppure
(x appartiene ad A) oppure 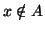 (x non appartiene ad A). Questa che può sembrare una richiesta ovvia
in realtà non lo è. Si consideri l'oggetto definito da:
(x non appartiene ad A). Questa che può sembrare una richiesta ovvia
in realtà non lo è. Si consideri l'oggetto definito da:
e si provi a stabilire se 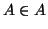 oppure no.
oppure no.
- 1.
- Se
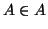 ,
allora, dalla definizione di A segue che
,
allora, dalla definizione di A segue che
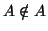
- 2.
- Se
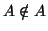 allora, per definizione di A,
allora, per definizione di A, 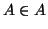
Quindi A non può essere un insieme, in quanto non possiamo decidere se 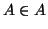 oppure no. Questo esempio è noto come il paradosso di Russel.
oppure no. Questo esempio è noto come il paradosso di Russel.
Il criterio per stabilire quando due insiemi sono uguali, è fornito dal
seguente
Assioma 1.1 (estensionalità)
Due insiemi sono uguali se e solo se hanno gli stessi elementi. In simboli
Definizione 1.2
Siano
X e
Y due insiemi, si dice che
X è
contenuto in
Y (o
anche
X è
sottinsieme di
Y), e si denota con
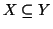
se
ogni elemento di
X è elemento di
Y, in simboli,
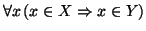
.
Si dice che
X è
contenuto strettamente in
Y (o anche che è un
sottinsieme proprio di
Y) e si denota con
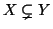
,
se
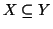
e
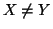
.
Un modo di definire degli insiemi è quello di usare una ``proprietà'' che ne
caratterizzi gli elementi. Ossia se P è una, formula della teoria
degli insiemi, per intenderci una proprietà esprimibile in
termini del simbolo di appartenenza e di uguaglianza, dei quantificatori e dei
connettivi logici, (e, o,
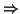 ,
non) allora con
,
non) allora con
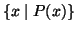 ,
si
intende la collezzione di tutti gli x che soddisfano la proprietà P. Il
paradosso di Russel mostra che in generale un tale oggetto può non essere un
insieme. Si dà però il seguente
,
si
intende la collezzione di tutti gli x che soddisfano la proprietà P. Il
paradosso di Russel mostra che in generale un tale oggetto può non essere un
insieme. Si dà però il seguente
Assioma 1.3 (separazione)
Se
X è un insieme e
P è una proprietà esprimibile in termini del
linguaggio della teoria degli insiemi, allora la collezione
è un insieme. Si userà spesso anche la notazione
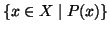
,
per
indicare questo insieme.
Definizione 1.4
Se
X e
Y sono insiemi si costruiscono altri insiemi:
Se
I è un insieme e per ogni
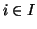
è dato un insieme
Xi, si
definiscono
- intersezione
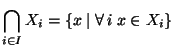
- unione
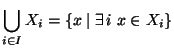
Osservazione 1.5
Quelle che abbiamo appena dato come definizioni, sono solo in parte tali. Se
infatti gli insiemi intersezione, differenza e complemento sono effettivamente
definibili a usando l'
assioma di separazione, per gli altri tale assioma non è più sufficiente
(non si separano degli elementi da un insieme, ma si costruiscono, insiemi
``più grandi'') e quindi tali costruzioni devono essere opportunamente
assiomatizzate, cosa che però noi non facciamo.
Esercizio 1.2
Siano
X e
Y insiemi, si provi che
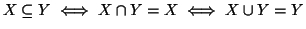
.
Soluzione
Esercizio 1.3
Siano
X,
Y,
Z insiemi, si provino le seguenti:
- 1.
- proprietà associativa dell'intersezione e dell'unione
- 2.
- proprietà commutativa
- 3.
- proprietà di assorbimento
- 4.
- proprietà distributiva dell'intersezione rispetto all'unione e
dell'unione rispetto all'intersezione
- 5.
- leggi di de Morgan
- 6.
-
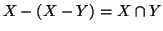
- 7.
- se
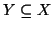 allora
allora
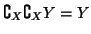 .
.
Soluzione
Esercizio 1.4
Siano
X,
Y,
Z insiemi, si provino le seguenti:
- 1.
-
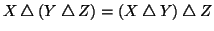
- 2.
-
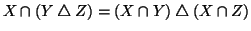
Soluzione
Relazioni, funzioni parziali e funzioni totali
Definizione 1.6
Siano
X e
Y insiemi si dice
relazione tra
X e
Y, un sottinsieme
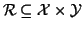
.
Se
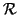
è una relazione si scriverà anche
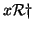
come sinonimo di
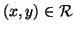
.
Una relazione tra X e se stesso, si dirà anche una relazione binaria
su X.
Definizione 1.7
Una relazione
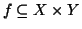
si dice una
funzione parziale se
per ogni
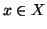
esiste al più un

tale che
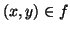
.
In
simboli:
Si scriverà
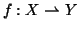
per dire che
f è una funzione parziale da
X a
Y e in tal caso si scriverà anche
y=
f(
x) come sinonimo di
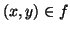
.
L'insieme
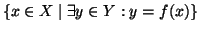
è detto il
dominio di
f e si denota con
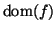
.
L'insieme
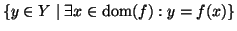 è detto
l'immagine di f e si denota con
è detto
l'immagine di f e si denota con
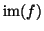 .
.
Una funzione parziale
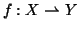 si dice funzione totale o
semplicemente funzione se
si dice funzione totale o
semplicemente funzione se
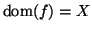 ,
in tal caso si scrive
,
in tal caso si scrive 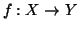 .
.
Si denota YX l'insieme di tutte le funzioni (totali) da X a Y, ossia
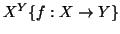 .
.
Osservazione 1.8
Una funzione parziale può essere pensata come ``una legge'' che ad
ogni elemento
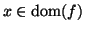
associa l'unico elemento

tale che
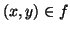
,
questo elemento si denota con
f(
x). Con questa
interpretazione, dà senso proprio all'uguale contenuto nella scrittura
y=
f(
x). In questa accezione (legge che associa ad un elemento un altro
elemento) verranno generalmente usate le funzioni.
Esempio 1.9
Se
X è un insieme
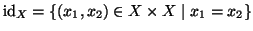
è una
funzione, che viene chiamata l'
identità di
X. In altri termini
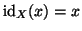
per ogni
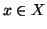
.
Definizione 1.10
Siano
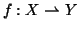
e
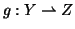
si chiama
composizione di
f e
g la
relazione tra
X e
Z definita da
Proposizione 1.11
Se
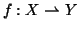
e
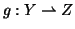
allora
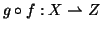
.
Se
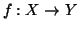
e
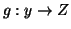
allora
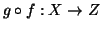
.
Dimostrazione.
Per provare il primo punto, dobbiamo mostrare che se
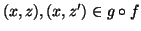 allora z=z'. Per definizione di
allora z=z'. Per definizione di 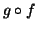 esiste
esiste  tale che y=f(x) e
z=g(y) ed esiste un
tale che y=f(x) e
z=g(y) ed esiste un 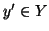 tale che y'=f(x) e z=g(y'). Ma allora, dato
che f è una funzione parziali, y=y', e quindi, dato che anche g è una
funzione parziale z=z').
tale che y'=f(x) e z=g(y'). Ma allora, dato
che f è una funzione parziali, y=y', e quindi, dato che anche g è una
funzione parziale z=z').
Se f e g sono funzioni totali, sono in particolare delle funzioni parziali e
quindi, per quanto appena mostrato, 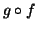 è una funzione
parziale. Dobbiamo provare che per ogni
è una funzione
parziale. Dobbiamo provare che per ogni 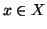 esiste uno
esiste uno 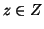 tale che
tale che
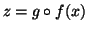 .
Sia
.
Sia 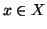 ,
dato che f `e una funzione totale, esiste
,
dato che f `e una funzione totale, esiste  tale che y=f(x), dato che anche g è totale esiste allora
tale che y=f(x), dato che anche g è totale esiste allora 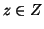 tale
che z=g(y), ma questo significa che
tale
che z=g(y), ma questo significa che
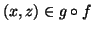 ,
ovvero
,
ovvero
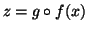 .
.

Osservazione 1.12
Con l'interpretazione data nell'osservazione
1.8 si ha allora che
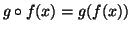
.
Definizione 1.13
Sia
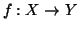
ed
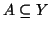
,
si chiamo
immagine inversa di
A tramite
f l'insieme:
Proposizione 1.15
Sia
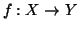
una bigezione, allora esiste una unica funzione
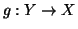
tale che
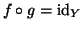
e
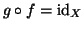
.
Tale funzione si chiama
inversa di
f e si denota con
f-1.
Dimostrazione.
Dato  esiste un unico
esiste un unico 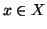 tale che f(x)=y (esiste perché fè surgettiva, è unico perché è iniettiva); chiamiamo g(y) tale
elemento. È allora evidente che f(g(y))=y per ogni
tale che f(x)=y (esiste perché fè surgettiva, è unico perché è iniettiva); chiamiamo g(y) tale
elemento. È allora evidente che f(g(y))=y per ogni  .
D'altra parte
f(g(f(x)))=f(x) per ogni
.
D'altra parte
f(g(f(x)))=f(x) per ogni 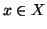 (applico la relazione precedente con
x=f(x)), e quindi per l'iniettività di f si ha che g(f(x))=x. È chiaro
che tale funzione è l'unica possibile con le proprietà richieste.
(applico la relazione precedente con
x=f(x)), e quindi per l'iniettività di f si ha che g(f(x))=x. È chiaro
che tale funzione è l'unica possibile con le proprietà richieste.

Il seguente esercizio inverte il risultato della proposizione precedente.
Esercizio 1.5
Sia
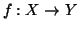
e si supponga che esista una funzione
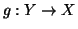
tale che
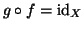
e
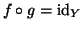
.
Si provi che allora
f è bigettiva.
Soluzione
Esercizio 1.6
Perché se
X e
Y sono insiemi allora anche
YX è un insieme?
Soluzione
Esercizio 1.7
Siano
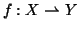
e
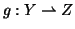
,
si determini
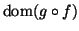
.
Soluzione
Esercizio 1.9
Siano
X,
Y,
I insiemi,
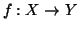
e
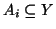
per ogni
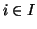
.
Si
provi che
Soluzione



Next: Lezione 2 (28 febbraio
Up: Matematica Discreta (II modulo)
Previous: Matematica Discreta (II modulo)
Domenico Luminati
2001-06-18
![]() (x appartiene ad A) oppure
(x appartiene ad A) oppure ![]() (x non appartiene ad A). Questa che può sembrare una richiesta ovvia
in realtà non lo è. Si consideri l'oggetto definito da:
(x non appartiene ad A). Questa che può sembrare una richiesta ovvia
in realtà non lo è. Si consideri l'oggetto definito da:
![]() ,
non) allora con
,
non) allora con
![]() ,
si
intende la collezzione di tutti gli x che soddisfano la proprietà P. Il
paradosso di Russel mostra che in generale un tale oggetto può non essere un
insieme. Si dà però il seguente
,
si
intende la collezzione di tutti gli x che soddisfano la proprietà P. Il
paradosso di Russel mostra che in generale un tale oggetto può non essere un
insieme. Si dà però il seguente![]() la differenza X-Y viene chiamata il complemento di Y in X e viene denotata anche con
la differenza X-Y viene chiamata il complemento di Y in X e viene denotata anche con
![]() o semplicemente con
o semplicemente con
![]() o con Y' quando non ci sia ambiguità
o con Y' quando non ci sia ambiguità
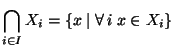
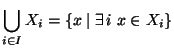
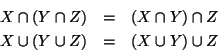
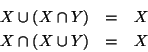
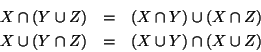
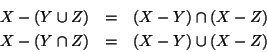
![]() è detto
l'immagine di f e si denota con
è detto
l'immagine di f e si denota con
![]() .
.
![]() si dice funzione totale o
semplicemente funzione se
si dice funzione totale o
semplicemente funzione se
![]() ,
in tal caso si scrive
,
in tal caso si scrive ![]() .
.
![]() .
.![]() allora z=z'. Per definizione di
allora z=z'. Per definizione di ![]() esiste
esiste ![]() tale che y=f(x) e
z=g(y) ed esiste un
tale che y=f(x) e
z=g(y) ed esiste un ![]() tale che y'=f(x) e z=g(y'). Ma allora, dato
che f è una funzione parziali, y=y', e quindi, dato che anche g è una
funzione parziale z=z').
tale che y'=f(x) e z=g(y'). Ma allora, dato
che f è una funzione parziali, y=y', e quindi, dato che anche g è una
funzione parziale z=z').
![]() è una funzione
parziale. Dobbiamo provare che per ogni
è una funzione
parziale. Dobbiamo provare che per ogni ![]() esiste uno
esiste uno ![]() tale che
tale che
![]() .
Sia
.
Sia ![]() ,
dato che f `e una funzione totale, esiste
,
dato che f `e una funzione totale, esiste ![]() tale che y=f(x), dato che anche g è totale esiste allora
tale che y=f(x), dato che anche g è totale esiste allora ![]() tale
che z=g(y), ma questo significa che
tale
che z=g(y), ma questo significa che
![]() ,
ovvero
,
ovvero
![]() .
.
![]()
![]() esiste un unico
esiste un unico ![]() tale che f(x)=y (esiste perché fè surgettiva, è unico perché è iniettiva); chiamiamo g(y) tale
elemento. È allora evidente che f(g(y))=y per ogni
tale che f(x)=y (esiste perché fè surgettiva, è unico perché è iniettiva); chiamiamo g(y) tale
elemento. È allora evidente che f(g(y))=y per ogni ![]() .
D'altra parte
f(g(f(x)))=f(x) per ogni
.
D'altra parte
f(g(f(x)))=f(x) per ogni ![]() (applico la relazione precedente con
x=f(x)), e quindi per l'iniettività di f si ha che g(f(x))=x. È chiaro
che tale funzione è l'unica possibile con le proprietà richieste.
(applico la relazione precedente con
x=f(x)), e quindi per l'iniettività di f si ha che g(f(x))=x. È chiaro
che tale funzione è l'unica possibile con le proprietà richieste.
![]()