


Next: Lezione 2 (24 febbraio
Up: Matematica Discreta
Previous: Matematica Discreta
Subsections
Assioma 1.1 (di buon ordinamento)
Se
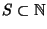
è un sottoinsieme non vuoto allora
S ha minimo,
ossia esiste
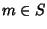
tale che per ogni
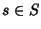
si ha
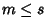
.
Teorema 1.2 (prima forma dell'induzione)
Sia
P(
n) una successione di proposizioni indicizzate sui naturali.
Si supponga che
- 1.
- P(0) sia vera.
- 2.
-
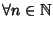
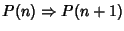
allora
P(
n) è vera per ogni
n.
Dim.
Sia
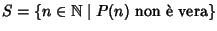 ,
se per assurdo
,
se per assurdo
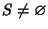 ,
per l'assioma di buon ordinamento esiste m il minimo di S. m>0dato che P(0) è vera per l'ipotesi 1, mentre P(m) è falsa in
quanto
,
per l'assioma di buon ordinamento esiste m il minimo di S. m>0dato che P(0) è vera per l'ipotesi 1, mentre P(m) è falsa in
quanto 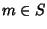 .
Ma allora
.
Ma allora
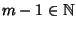 e, dato che m-1<m e m è
il minimo di S,
e, dato che m-1<m e m è
il minimo di S,
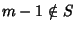 ossia P(m-1) è vera. Ma allora,
per l'ipotesi 2 si ha che
P(m-1+1)=P(m) è vera, ossia
ossia P(m-1) è vera. Ma allora,
per l'ipotesi 2 si ha che
P(m-1+1)=P(m) è vera, ossia 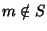 ,
che è assurdo. Quindi
,
che è assurdo. Quindi
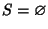 ossia P(n) è vera per ogni
ossia P(n) è vera per ogni
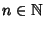 .
.

Teorema 1.3 (seconda forma dell'induzione)
Sia
P(
n) una successione di proposizioni indicizzate sui naturali.
Si supponga che
- 1.
- P(0) sia vera.
- 2.
-
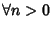 se P(k) è vera per ogni k<n allora anche
P(n) è vera
se P(k) è vera per ogni k<n allora anche
P(n) è vera
allora
P(
n) è vera per ogni
n.
Dim.
Come nella dimostrazione precedente sia
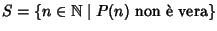 ,
e come prima supponiamo per assurdo
,
e come prima supponiamo per assurdo
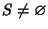 ,
e sia m il minimo di S. m>0 dato che P(0)è vera per l'ipotesi 1, mentre P(m) non è vera in quanto
,
e sia m il minimo di S. m>0 dato che P(0)è vera per l'ipotesi 1, mentre P(m) non è vera in quanto 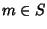 .
Inoltre, dato che m è il minimo di S, se k<m allora
.
Inoltre, dato che m è il minimo di S, se k<m allora
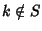 e quindi P(k) è vera. Ma allora, per l'ipotesi 2 si ha
che P(m) è vera, ossia
e quindi P(k) è vera. Ma allora, per l'ipotesi 2 si ha
che P(m) è vera, ossia 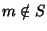 ,
che è assurdo. Quindi
,
che è assurdo. Quindi
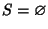 ossia P(n) è vera per ogni
ossia P(n) è vera per ogni
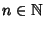 .
.

Dim.
Usiamo il principio di induzione nella seconda forma applicato alla successione di proposizioni
Se n=0 basta prendere q=r=0. Sia ora n>0 e supponiamo che P(k)sia vera per ogni k<n. Osserviamo che se m> n basta prendere
q=0 e r=n. Se invece 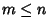 ,
consideriamo k=n-m. Dato che
,
consideriamo k=n-m. Dato che
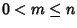 si ha
si ha 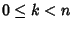 e quindi, per ipotesi di induzione P(k)è vera. Ossia esistono
e quindi, per ipotesi di induzione P(k)è vera. Ossia esistono
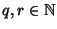 tali che
tali che 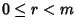 e k=mq+r.
Ma allora
n=k+m=mq+m+r=m(q+1)+r.
e k=mq+r.
Ma allora
n=k+m=mq+m+r=m(q+1)+r.




Next: Lezione 2 (24 febbraio
Up: Matematica Discreta
Previous: Matematica Discreta
Domenico Luminati
1999-07-08
![]() ,
se per assurdo
,
se per assurdo
![]() ,
per l'assioma di buon ordinamento esiste m il minimo di S. m>0dato che P(0) è vera per l'ipotesi 1, mentre P(m) è falsa in
quanto
,
per l'assioma di buon ordinamento esiste m il minimo di S. m>0dato che P(0) è vera per l'ipotesi 1, mentre P(m) è falsa in
quanto ![]() .
Ma allora
.
Ma allora
![]() e, dato che m-1<m e m è
il minimo di S,
e, dato che m-1<m e m è
il minimo di S,
![]() ossia P(m-1) è vera. Ma allora,
per l'ipotesi 2 si ha che
P(m-1+1)=P(m) è vera, ossia
ossia P(m-1) è vera. Ma allora,
per l'ipotesi 2 si ha che
P(m-1+1)=P(m) è vera, ossia ![]() ,
che è assurdo. Quindi
,
che è assurdo. Quindi
![]() ossia P(n) è vera per ogni
ossia P(n) è vera per ogni
![]() .
.
![]()
![]() ,
e come prima supponiamo per assurdo
,
e come prima supponiamo per assurdo
![]() ,
e sia m il minimo di S. m>0 dato che P(0)è vera per l'ipotesi 1, mentre P(m) non è vera in quanto
,
e sia m il minimo di S. m>0 dato che P(0)è vera per l'ipotesi 1, mentre P(m) non è vera in quanto ![]() .
Inoltre, dato che m è il minimo di S, se k<m allora
.
Inoltre, dato che m è il minimo di S, se k<m allora
![]() e quindi P(k) è vera. Ma allora, per l'ipotesi 2 si ha
che P(m) è vera, ossia
e quindi P(k) è vera. Ma allora, per l'ipotesi 2 si ha
che P(m) è vera, ossia ![]() ,
che è assurdo. Quindi
,
che è assurdo. Quindi
![]() ossia P(n) è vera per ogni
ossia P(n) è vera per ogni
![]() .
.
![]()