Soluzioni proposte

Soluzione dell'esercizio 1  Le rette L e M sono incidenti nel punto P=(1,0) e le rette L' e M'sono incidenti nel punto P'=(0,1). Per ottenere un'affinità con le proprietà richieste è sufficiente determinarne una tale che $\varphi(P)=P'$ e tale che la sua parte lineare porti le direzioni delle rette L e M in quelle di L' e M' cosa che è possibile, perché tali direzioni sono indipendenti. Dei vettori direzione per le rette L, M , L', M' sono rispettivamente:

$$\begin{array}{rclcrcl} v & = & (1,-1), &\quad w & = & (1,1) \\ v' & = & (1,0), &\quad w' & = & (1,2) \end{array}$$

L'applicazione lineare che porti v su v' e w su w' è allora data dalla matrice

$$A=\left( \begin{array}{cc} 1 & 1 \\ 0 & 2 \end{array}\ri... ...left( \begin{array}{cc} 1 & 0 \\ 1 & 1 \end{array}\right)$$

Ma allora l'affinità cercata sarà $\varphi(X)= A (X-P) + P' = A X +P' - AP$, ossia

$$\begin{array}{rcl} \varphi(x,y) & = & \left( \begin{array}{... ... \begin{array}{c} x-1 \\ x + y \end{array}\right) \end{array}$$

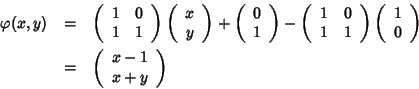
L'affinità cercata non è unica. Diverse scelte dei vettori direzione delle rette portano alla costruzione di una diversa affinità con la stessa proprietà, ad esempio scegliendo

$$\begin{array}{rclcrcl} v & = & (1,-1), &\quad w & = & (1,1) \\ v' & = & (1,0), &\quad w' & = & (2,4) \end{array}$$

come vettori direzione, si ottiene l'affinità $\varphi(x,y) =(3x/2 +y/2-3/2,2x+2y-1)$, che è diversa dalla precedente.

Una isometria con le proprietà volute non può esistere in quanto le due rette L e M sono ortogonali, mentre L' e M' no ( $\langle v,w\rangle=0$, mentre $\langle v',w'\rangle=1\ne 0$).     

Soluzione dell'esercizio 2  La retta r può essre scritta in forma parametrica come $\{t(-2,3,1)+(3,1,0)\mid t\in\mathbb R\}$ e quindi un vettore direzione per r è il vettore v=(-2,3,1).

1. La retta s è parallela alla retta r (hanno la stessa direzione e non coincidono in quanto è immediato che $(1,1,1)\in s$ ma $(1,1,1)\not\in r$) quindi ogni piano passante per r, tranne quello che contiene s ha la proprietà cercata, ad esempio il piano di equazione y-3z=1 (non contiene sin quanto non contiene il punto (1,1,1)).

2. Se $\Sigma$ è un piano contenente r e parallelo a $\Pi$, allora la direzione di r è ortogonale alla normale a $\Sigma$, che coincide con la normale a $\Pi$. Ma una normale a $\Pi$ è il vettore w=(1,1,1) e $\langle v,w\rangle=-2+3+1=2\ne0$, quindi un siffatto piano $\Sigma$ non esiste.

3. Il fascio di piani passante per r ha equazione

$$\alpha ( x + 2z - 3 ) + \beta ( y - 3z -1 ) = 0$$

ossia $\alpha x + \beta y + ( 2\alpha - 3 \beta )z = 3 \alpha + \beta$ che ha per normale il vettore $u_{\alpha,\beta} = (\alpha,\beta,2\alpha - 3 \beta)$. Perché un tale piano risulti normale a $\Pi$ dovrà risultare $\langle u_{\alpha,beta},w\rangle=0$ ossia

$$0=\langle (\alpha,\beta,2\alpha - 3\beta),(1,1,1)\rangle=3\alpha-2\beta$$

ovvero $(\alpha,\beta)=\lambda(2,3)$. Il piano cercato esiste ed è unico ed ha equazione 2 x + 3 y -5z = 9.     

Soluzione dell'esercizio 3  Il fascio di coniche ha equazione

$$\alpha y ( x - 2 ) +\beta(y-x)(y-x+1) = 0$$

ossia

$$\beta x^2 + \beta y^2 +(\alpha - 2\beta) xy - \beta x + (\beta - 2\alpha) y = 0$$

La matrice di questa conica è data da:

$$\left( \begin{array}{cc\vert c} \beta & (\alpha-2\beta)/2 &... ...hline -\beta/2 & (\beta - 2\alpha)/2 & 0 \end{array} \right)$$

Il determinante della parte quadratica è $\beta^2 -(\alpha - 2\beta)^2/4=-\alpha(\alpha -4\beta)/4$ che si annulla se e solo se $\alpha=0$oppure $\alpha=4\beta$. Se $\alpha=0$ la conica è una coppia di rette parallele ( (y-x)(y-x+1) = 0), se $\alpha=4$ e $\beta=1$ la matrice della conica si riduce invece a:

$$\left( \begin{array}{cc\vert c} 1 & 1 & -1/2 \\ 1 & 1 & -7/2 \\ \hline -1/2 & -7/2 & 0 \end{array} \right)$$

che ha determinante pari a -9 e quindi è non degenere, la conica e per tanto una parabola.

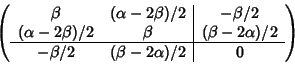
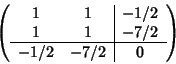
Perché la conica sia una circonferenza deve aversi $(\alpha-2\beta)/2=0$ e quindi $\alpha=2$ e $\beta=1$, nel qual caso la matrice diventa

$$\left( \begin{array}{cc\vert c} 1 & 0 & -1/2 \\ 0 & 1 & -3/2 \\ \hline -1/2 & -3/2 & 0 \end{array} \right)$$

che ha determinante $-5/2 \ne 0$ e quindi è non degenere, la conica e per tanto una circonferenza.     

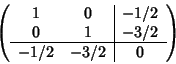
Soluzione dell'esercizio 4  Sia e₁, e₂ e e₃ i vettori della base standard di $\mathbb R^3$ rispetto a cui è scritta la matrice del prodotto scalare ed usiamo il metodo di Jacobi per la determinazione di una base ortogonale.

Poniamo

$$\begin{eqnarray*}v_1 & = & e_1 \\ v_2 & = & e_2 - \frac{\langle e_2,e_1\rangle... ...c{\langle e_3,e_1\rangle}{\langle e_1,e_1\rangle}e_1 = e_3 + e_1 \end{eqnarray*}$$

risulta:

$$\begin{eqnarray*}\langle v_2,v_2\rangle & = & \langle e_2,e_2\rangle + 4 \langle... ...angle e_1,e_1\rangle + 2 \langle e_1,e_2\rangle = 1 + 1 - 2 = 0 \end{eqnarray*}$$

Quindi rispetto a questa base la matrice associata al prodotto scalare è:

$$\left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 0 & 3 \\ 0 & 3 & 0 \end{array} \right)$$

Consideriamo ora la base

$$\begin{eqnarray*}w_1 & = & v_1 \\ w_2 & = & v_2 - v_3 \\ w_3 & = & v_2 + v_3 \end{eqnarray*}$$

risulta:

$$\begin{eqnarray*}\langle w_2,w_2\rangle & = & \langle v_2,v_2\rangle + \langle v... ...\rangle + \langle v_3,v_3\rangle + 2 \langle v_2,v_3\rangle = 6 \end{eqnarray*}$$

Quindi rispetto a questa base la matrice associata al prodotto scalare è:

$$\left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & -6 & 0 \\ 0 & 0 & 6 \end{array} \right)$$

L'indice di positività del prodotto scalare è 2 e quello di negatività è -1, e la base

$$\begin{eqnarray*}w_1 & = & v_1 = e_1 = (1,0,0)\\ w_2 & = & v_2 - v_3 = e_2 - 3... ...3 = (-3,1,-1)\\ w_3 & = & v_2 + v_3 = e_2 -e_1 +e_3 = (-1,1,1) \end{eqnarray*}$$

è una base ortogonale.     

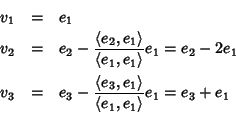
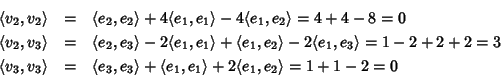
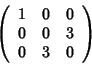
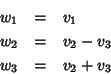
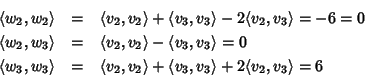
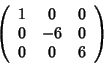
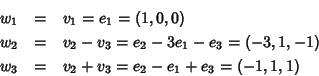
Soluzione dell'esercizio 5  Proviamo le due inclusioni.

$\ker F^* \subseteq (F(V))^\perp$. Sia $u\in\ker F^*$ e sia $w\in F(V)$, allora esiste $v\in V$ tale che F(v)=w e quindi:

$$\langle u,w\rangle=\langle u,F(v)\rangle=\langle F^*(u),v\rangle=\langle 0,v\rangle=0$$

e quindi per l'arbitrarietà di $W\in F(V)$ si ha che $u\in (F(V))^\perp$.

$\ker F^* \supseteq (F(V))^\perp$. Sia $u\in (F(V))^\perp$, allora, per ogni $v\in V$ si ha che $\langle u,F(v)\rangle=0$, e quindi $\langle F^*(u),v\rangle=0$ per ogni $v\in V$. Dato che il prodotto scalare è non degenere, ciò implica che F^*(u)=0 ossia che $u\in\ker F^*$.