



Next: Results
Up: BEC-BCS crossover
Previous: Introduction
Contents
The homogeneous two-component Fermi gas is described by the Hamiltonian
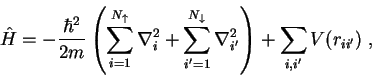 |
(9.2) |
where 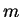 denotes the mass of the particles,
denotes the mass of the particles, 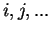 and
and
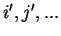 label, respectively, spin-up and spin-down particles and
label, respectively, spin-up and spin-down particles and
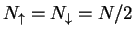 ,
, 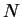 being the total number of atoms. We model the
interspecies interatomic interactions using an attractive square-well potential:
being the total number of atoms. We model the
interspecies interatomic interactions using an attractive square-well potential:
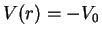 for
for 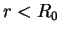 , and
, and 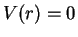 otherwise. In order to ensure that the mean
interparticle distance is much larger than the range of the potential we use
otherwise. In order to ensure that the mean
interparticle distance is much larger than the range of the potential we use
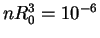 , where
, where
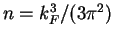 is the gas number density. By varying the
depth
is the gas number density. By varying the
depth 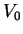 of the potential one can change the value of the
of the potential one can change the value of the 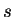 -wave scattering
length, which for this potential is given by
-wave scattering
length, which for this potential is given by
![$a=R_0[1-\tan(K_0R_0)/(K_0R_0)]$](img1760.gif) , where
, where
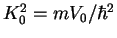 . We vary
. We vary 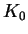 is the range:
is the range: 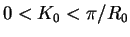 . For
. For
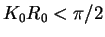 the potential does not support a two-body bound state and
the potential does not support a two-body bound state and 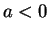 . For
. For
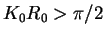 , instead, the scattering length is positive,
, instead, the scattering length is positive, 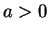 , and a molecular
state appears whose binding energy
, and a molecular
state appears whose binding energy 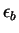 is determined by the trascendental
equation
is determined by the trascendental
equation
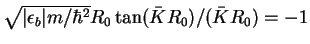 , where
, where
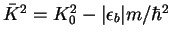 . The value
. The value
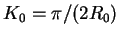 corresponds to
the unitary limit where
corresponds to
the unitary limit where 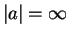 and
and 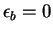 .
.
In the present study we resort to the Fixed Node Monte Carlo technique described in
Sec. 2.4. We make use of the following trial wave functions. A BCS wave
function
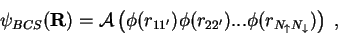 |
(9.3) |
and a Jastrow-Slater (JS) wave function
![\begin{displaymath}
\psi_{JS}({\bf R})=\prod_{i,i^\prime}\varphi(r_{ii^\prime}) ...
...\alpha}
e^{i{\bf k}_\alpha\cdot{\bf r}_{i^\prime}} \right] \;,
\end{displaymath}](img1773.gif) |
(9.4) |
where 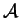 is the antisymmetrizer operator ensuring the correct antisymmetric
properties under particle exchange. In the JS wave function, Eq. (9.4), the
plane wave orbitals have wave vectors
is the antisymmetrizer operator ensuring the correct antisymmetric
properties under particle exchange. In the JS wave function, Eq. (9.4), the
plane wave orbitals have wave vectors
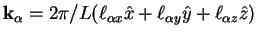 , where
, where 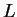 is the size of the periodic cubic box fixed by
is the size of the periodic cubic box fixed by 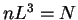 ,
and
,
and 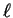 are integer numbers. The correlation functions
are integer numbers. The correlation functions 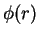 and
and 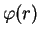 in Eqs. (9.3)-(9.4) are constructed from solutions of the two-body
Schrödinger equation with the square-well potential
in Eqs. (9.3)-(9.4) are constructed from solutions of the two-body
Schrödinger equation with the square-well potential 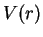 . In particular, in the
region
. In particular, in the
region 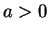 we take for the function
we take for the function 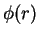 the bound-state solution
the bound-state solution
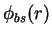 with energy
with energy 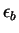 and in the region
and in the region 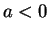 the unbound-state
solution corresponding to zero scattering energy:
the unbound-state
solution corresponding to zero scattering energy:
![$\phi_{us}(r)=(R_0-a)\sin(K_0r)/[r\sin(K_0R_0)]$](img1781.gif) for
for 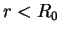 and
and
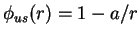 for
for 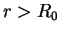 . In the unitary limit,
. In the unitary limit, 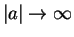 ,
,
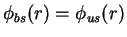 .
.
The JS wave function 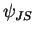 , Eq. (9.4), is used only in the region of
negative scattering length,
, Eq. (9.4), is used only in the region of
negative scattering length, 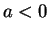 , with a Jastrow factor
, with a Jastrow factor
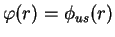 for
for 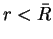 . In order to reduce possible size effects due to the long range tail
of
. In order to reduce possible size effects due to the long range tail
of 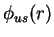 , we have used
, we have used
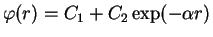 for
for 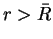 ,
with
,
with 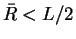 a matching point. The coefficients
a matching point. The coefficients 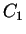 and
and 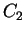 are fixed by
the continuity condition for
are fixed by
the continuity condition for 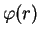 and its first derivative at
and its first derivative at 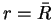 ,
whereas the parameter
,
whereas the parameter 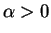 is chosen in such a way that
is chosen in such a way that 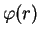 goes
rapidly to a constant. Residual size effects have been finally determined carrying
out calculations with an increasing number of particles
goes
rapidly to a constant. Residual size effects have been finally determined carrying
out calculations with an increasing number of particles 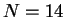 , 38, and 66. In the
inset of Fig. 9.1 we show the dependence of the energy per particle
, 38, and 66. In the
inset of Fig. 9.1 we show the dependence of the energy per particle
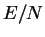 on
on 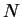 in the unitary limit. Similar studies carried out in the BEC and BCS
regime show that the value
in the unitary limit. Similar studies carried out in the BEC and BCS
regime show that the value 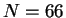 is optimal since finite-size corrections in the
energy are below the reported statistical error in the whole BEC-BCS crossover. We
have also checked that effects due to the finite range
is optimal since finite-size corrections in the
energy are below the reported statistical error in the whole BEC-BCS crossover. We
have also checked that effects due to the finite range 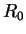 of the potential are
negligible.
of the potential are
negligible.
Figure:
Energy per particle in the BEC-BCS crossover. Solid symbols refer to
results obtained with the trial wave function 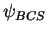 , open symbols refer to
the ones obtained with
, open symbols refer to
the ones obtained with 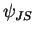 . The red dot-dashed line is the expansion
(9.5) holding in the BCS region and the blue dotted line corresponds to the
binding energy
. The red dot-dashed line is the expansion
(9.5) holding in the BCS region and the blue dotted line corresponds to the
binding energy 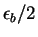 . Inset: finite size effects in the unitary limit
. Inset: finite size effects in the unitary limit
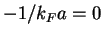 .
.
|
|




Next: Results
Up: BEC-BCS crossover
Previous: Introduction
Contents
G.E. Astrakharchik
15-th of December 2004
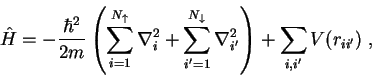
![]() , Eq. (9.4), is used only in the region of
negative scattering length,
, Eq. (9.4), is used only in the region of
negative scattering length, ![]() , with a Jastrow factor
, with a Jastrow factor
![]() for
for ![]() . In order to reduce possible size effects due to the long range tail
of
. In order to reduce possible size effects due to the long range tail
of ![]() , we have used
, we have used
![]() for
for ![]() ,
with
,
with ![]() a matching point. The coefficients
a matching point. The coefficients ![]() and
and ![]() are fixed by
the continuity condition for
are fixed by
the continuity condition for ![]() and its first derivative at
and its first derivative at ![]() ,
whereas the parameter
,
whereas the parameter ![]() is chosen in such a way that
is chosen in such a way that ![]() goes
rapidly to a constant. Residual size effects have been finally determined carrying
out calculations with an increasing number of particles
goes
rapidly to a constant. Residual size effects have been finally determined carrying
out calculations with an increasing number of particles ![]() , 38, and 66. In the
inset of Fig. 9.1 we show the dependence of the energy per particle
, 38, and 66. In the
inset of Fig. 9.1 we show the dependence of the energy per particle
![]() on
on ![]() in the unitary limit. Similar studies carried out in the BEC and BCS
regime show that the value
in the unitary limit. Similar studies carried out in the BEC and BCS
regime show that the value ![]() is optimal since finite-size corrections in the
energy are below the reported statistical error in the whole BEC-BCS crossover. We
have also checked that effects due to the finite range
is optimal since finite-size corrections in the
energy are below the reported statistical error in the whole BEC-BCS crossover. We
have also checked that effects due to the finite range ![]() of the potential are
negligible.
of the potential are
negligible.
![\includegraphics[width=0.6\textwidth]{figBECBCS1.eps}](figBECBCS1.gif)