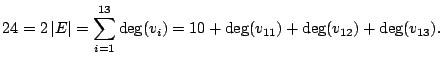: この文書について...
: Matematica Discreta (II modulo)
: Matematica Discreta (II modulo)
Soluzione dell'esercizio 1  quindi
quindi 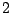 è invertibile
è invertibile
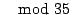 . Inoltre
. Inoltre
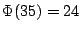 e
e 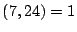 , quindi la congruenza è risolubile. Un
inverso di
, quindi la congruenza è risolubile. Un
inverso di 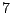
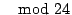 è dato da
è dato da 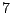 e quindi le soluzioni della
congruenza sono date da
e quindi le soluzioni della
congruenza sono date da
![$ \left[2^7\right]_{35}=\left[23\right]_{35}$](img23.gif) .
.
Il sistema è quindi equivalente a
che non ha soluzione dato che
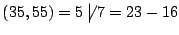 .
.

Soluzione dell'esercizio 2 Diamo solo i risultati, per la prova si veda la soluzione dell'analogo
esercizio nell'altro compito di questo appello.
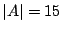 e
e
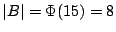 .
.
(1).
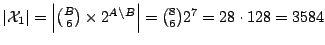 .
.
(2).
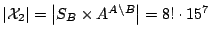 .
.
(3).
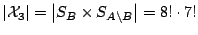 .
.

Soluzione dell'esercizio 3 In 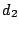 ci sono un numero dispari di numeri dispari, quindi non può
essere lo score di un grafo.
ci sono un numero dispari di numeri dispari, quindi non può
essere lo score di un grafo.
Per 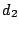 usiamo il teorema dello score:
usiamo il teorema dello score:
Dato che 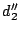 è realizzabile come score di un grafo, anche
è realizzabile come score di un grafo, anche 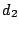 lo è. La
costruzione standard produce il grafo in figura che è sconnesso.
lo è. La
costruzione standard produce il grafo in figura che è sconnesso.
Figura:
Il grafo costruito per la soluzione dell'esercizio 3. La
configurazione di partenza è data dai vertici e lati neri a
cui si aggiungono nell'ordine quelli rossi e quelli blu.
 |
(1).
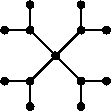
La risposta è sì. Ad esemoio quello in figura.
Figura:
Un albero che realizza lo score 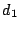 dell'esercizio 3.
dell'esercizio 3.
 |
(2).
La risposta è sì. Ad esempio quello in figura.
(3).
La risposta è no. Un grafo hamiltoniano ha tutti i vertici di grado
almeno 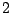 .
.

Soluzione dell'esercizio 4 Sia 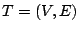 un tale albero e sia
un tale albero e sia
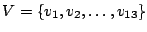 con
con
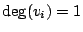 per
per
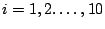 . Allora dato che
. Allora dato che 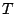 è un albero
è un albero
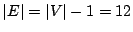 e quindi
e quindi
Se non ci fossero vertici di grado 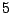 allora si avrebbe che
allora si avrebbe che
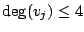 per ogni
per ogni 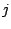 e dalla relazione precedente si otterrebbe:
che è un assurdo.
e dalla relazione precedente si otterrebbe:
che è un assurdo.




: この文書について...
: Matematica Discreta (II modulo)
: Matematica Discreta (II modulo)
domenico luminati
平成17年9月7日
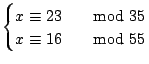
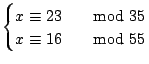
![]() e
e
![]() .
.
![]() .
.
![]() .
.
![]() ci sono un numero dispari di numeri dispari, quindi non può
essere lo score di un grafo.
ci sono un numero dispari di numeri dispari, quindi non può
essere lo score di un grafo.
![]() usiamo il teorema dello score:
usiamo il teorema dello score:
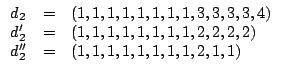
![]() .
.
![]()
![]() un tale albero e sia
un tale albero e sia
![]() con
con
![]() per
per
![]() . Allora dato che
. Allora dato che ![]() è un albero
è un albero
![]() e quindi
e quindi