Soluzioni proposte

Soluzione dell'esercizio 1 $23$ è primo, quindi $2$ è invertibile $\quad{\rm mod}\ 23$. Inoltre $\Phi(23)=22$ e $(5,22)=1$, quindi la congruenza è risolubile. Un inverso di $5$ $\quad{\rm mod}\ 22$ è dato da $9$ e quindi le soluzioni della congruenza sono date da $\left[2^9\right]_{23}=\left[6\right]_{23}$.     

Soluzione dell'esercizio 2 (1). $4=\left\vert{A \choose 3}\right\vert = {\left\vert A\right\vert \choose 3}={n \choose 3} = n(n-1)(n-2)/6$ se e solo se $n(n-1)(n-2)=24$. Dato che gli unici tre numeri consecutivi il cui prodotto fa $24$ sno $2$, $3$ e $4$, si ha che $n=4$.

(2). Se $n$ è pari, anche $n-2$ lo è, quindi $4 \mathrel{\big\vert}n(n-1)(n-2)$. Dato che anche $3 \mathrel{\big\vert}n(n-1)(n-2)$ e $(3,4)=1$ allora $12 \mathrel{\big\vert}n(n-1)(n-2)$ e quindi $2 \mathrel{\big\vert} n(n-1)(n-2)/6$.

(3) (4). Se $n$ è dispari allora anche $n-2$ lo è, quindi $2 \mathrel{\big\vert} n(n-1)(n-2)/6$ se e solo se $4\mathrel{\big\vert}n-1$. Infatti $2 \mathrel{\big\vert} n(n-1)(n-2)/6$ se e solo se $4 \mathrel{\big\vert}n(n-1)(n-2)$ e dato che $n(n-2)$ è dispari, questo si verifica se e solo se $4\mathrel{\big\vert} (n-1)$ ossia se e solo se $n \cong 1 \quad{\rm mod}\ 4$.

In particolare il numero $5$ risponde alla domanda (3).     

Soluzione dell'esercizio 3 Se $G=(V,E)$ è un grafo tale che $\mathop{\rm score}\nolimits (G)=d_1$ allora $\left\vert V\right\vert=10$ e ci sono due vertci di grado $8$, chiamiamoli $u$ e $v$. Ma allora i vertci che sono adiacenti sia a $u$ che a $v$ devono essere almeno $6$ (in un insieme con $10$ elementi due sottinsiemi dicardinalità $8$ hanno intersezione di cardinalità almeno $8+8-10=6$) e quindi ci dovrebbero essere almeno $6$ vertici diversi da $u$ e $v$ con grado almeno $2$.. Ciò è in contraddizione con il fatto che di vertici di grado $\ge 2$ e diversi da $u$ e $v$ ce ne dovrebbero essere soltanto $5$.

Per $d_2$ usiamo il teorema dello score:

$$\begin{array}{lcl} d_2 & = & (3, 3, 3, 3, 4, 4, 6, 7, 7)\\ d_2' ... ...d_2'' & = & (1, 1, 2, 2, 2, 2, 4)\\ d_2'''& = & (1, 1, 1, 1, 1, 1) \end{array}$$

Dato che $d_2'''$ è realizzabile come score di un grafo, anche $d_1$ lo è. La costruzione standard produce il grafo in figura che è $2$-connesso.

Figura 1: Il grafo costruito per la soluzione dell'esercizio 3. La configurazione di partenza è data dai vertici e lati neri a cui si aggiungono nell'ordine quelli rossi, blu e verdi.

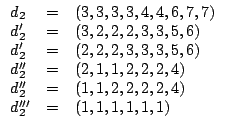
(1). La risposta è no. Ogni albero finito ha vertici di grado $1$, mentre in un tale grafo ogni vertice ha grado $\ge 2$..

(2). La risposta è no. Se $G=(V,E)$ è un grafo tale che $\mathop{\rm score}\nolimits (G)=d_1$ allora esiste $v\in V$ tale che $\deg(V)=8$, ossia ogni altro vertice, tranne uno, è adiacente e quindi congiungibile con $v$. D'altra parte l'unico vertice non ancora considerato ha grado positivo, e quindi deve essere congiungibile con almeno uno degli altri. Quindi $G$ è connesso.

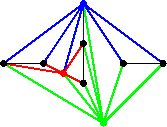
(3). Che il grafo di figura 1 sia $2$-connesso lo si può vedere ad esempio mostrando che è ottenuto da un ciclo con successive aggiunzioni e suddivisioni di lati.     

Soluzione dell'esercizio 4 I primi due grafi sono tra loro isomorfi. In realtà sono isomorfi entrambi al grafo costituito dagli spigoli di un cubo, in cui i vertici sono terne $(x,y,z)$ con $x,y,z\in\{0,1\}$ ed in cui i lati sono le coppie di vertici che differiscono esattamente in una sola coordinata. Con una tale descrizione, non è difficile provare che in questo grafo non ci sono $3$-cicli. Infatti due vertici (terne di zeri e uni) che sono entrambi adiacenti ad un terzo vertice, devono differire da quest'ultimo ciascuno in una coordinate e quindi differiascono tra loro in due coordinate e pertanto non sono adiacenti. In simboli se $(x',y',z')$ e $(x'',y'',z'')$ sono entrambi adiacenti a $(x,y,z)$ allora, senza ledere la generalità, possiamo supporre che $y'=y$ e $z'=z$ e $x'\ne x$ e $x''=x$ e $z''=z$ e $y''\ne y$. Ma allora $x'\ne x''$ e $y'\ne y''$, ossia $(x',y',z')$ e $(x'',y'',z'')$ non sono adiacenti.

Ma allora, dato che il terzo grafo contiene evidentemente dei $3$-cicli, i primi due grafi non sono isomorfi al terzo.

Un altro modo per provare che nei primi due grafi non ci sono $3$-cicli poteva essere quello di usare la matrice di adiacenza che ha una forma molto particolare e di cui non è difficile calcolare le potenze.