Soluzioni proposte

Soluzione dell'esercizio 1  La distanza fra un punto (x₀,y₀) e una retta di equazione ax+by+c=0 è data dalla formula

$$\frac{\left\vert a x_0 + b y_0 + c\right\vert}{\sqrt{a^2+b^2}}$$

Si ottiene perciò

$$d(P,L)=2/\sqrt{2}, \qquad\qquad d(Q,M)=\sqrt{2}/1,$$

e quindi $d(P,L)=d(Q,M)=\sqrt{2}$.

Sia $\sigma$ la riflessione attorno all'asse delle y, allora evidentemente $\sigma(Q)=Q$ e $\sigma(L)=L$, quindi se $\varphi$ è una isometria con le proprietà richieste, allora anche $\sigma \circ \varphi$ ha le stesse proprietà e $\sigma\circ\varphi\ne\varphi$, quindi se una tale isometria esiste, non è unica.

Una generica isometria che porta il punto P su Q è del tipo

$$\varphi(X)= A(X-P)+Q$$

con A una matrice ortogonale. Se si vuole che $\varphi(L)=M$, allora la matrice A dovrà portare la giacitura di L su quella di M e il vettore P₀-Psul vettore Q₀-Q essendo $P_0\in L$ e $Q_0\in M$ i punti delle due rette che realizzano la minima distanza rispettivamente da P e Q. Una semplice verifica mostra che P₀=(1,0) e $Q_0=(0,\sqrt 2)$ e che la giacitura della retta L è data da $V_L=\left\langle {}(1,1)\right\rangle$ mentre la giacitura di M è data da $V_M=\left\langle {}(1,0)\right\rangle$.

Indichiamo con v_l e v_M dei generatori, di norma unitaria, delle due giacitura, ad esempio $v_L=(\sqrt2/2,\sqrt2/2)$ e v_M=(1,0) e con $u_L=(P_0-P)/\left\Vert P_0-P\right\Vert=(\sqrt 2/2,-\sqrt2/2)$ e $v_M=(Q_0-Q)/\left\Vert Q_0-Q\right\Vert= (0,1)$

Le condizioni su A sono allora equivalenti a richiedere che

$$Av_L=v_M \quad \hbox{\rm {e}} \quad Au_L=\pm u_M$$

ossia

$$A\left( \begin{array}{c} \sqrt2/2\\ -\sqrt2/2 \end{array}\... ...ight) = \left( \begin{array}{c} \pm1\\ 0 \end{array}\right)$$

da cui segue che

$$A=\left( \begin{array}{cc} \sqrt2/2 & \sqrt2/2 \\ \sqrt2/... ...t2/2 & -\sqrt2/2 \\ \sqrt2/2 & -\sqrt2/2 \end{array}\right)$$

Si ottengono per tanto esattamente due isometrie che verificano le condizioni richieste e precisamente

$$\varphi_1(x,y)=\left( \begin{array}{cc} \sqrt2/2 & \sqrt2/2... ... (x+y)/\sqrt2 -\sqrt2 \\ (x - y)/\sqrt2 \end{array}\right)$$

e

$$\varphi_2(x,y)=\left( \begin{array}{cc} -\sqrt2/2 & -\sqrt2... ...(x+y)/\sqrt2 + \sqrt2 \\ (x - y)/\sqrt2 \end{array}\right).$$

Si osservi che ciascuna delle due isometrie trovate è la composizione dell'altra con la riflessione attorno all'asse delle y, che è l'unica riflessione non banale che porta la seconda configurazione su se stessa.     

Soluzione dell'esercizio 2  La retta r può essere scritta in forma parametrica come:

$$r=\{(2-t,2t+1,t)\mid t \in \mathbb R\}$$

e quindi un vettore direzione per r è v=(-1,2,1).

Osserviamo che un piano come nel punto 3) non può esistere, infatti se esistesse la direzione di r e la direzione di s dovrebbero essere ortogonali, ma un vettore direzione per s è w=(-1,2,-2) e $\langle v,w\rangle=1+4-2=3\ne0$.

Il punto P appartiene alla retta r, quindi ogni piano passante per la retta contiene anche P ad esempio il piano di equazione x+z=2. Chiaramente tale piano non è unico.

Date due rette sghembe esiste un unico piano passante per l'una e parallelo all'altra. Le rette r e s sono sghembe, infatti le loro direzioni sono linearmente indipendenti e non hanno intersezione in quanto il sistema

$$\left\{ \begin{array}{l} (1-t)+(1-2t)=2 \\ (1+2t)-2(1-2t)... ... \left\{ \begin{array}{l} t=0 \\ t=1/3 \end{array}\right.$$

non ha soluzione. Quindi esiste un unico piano come al punto 2). Determiniamolo. L'equazione del fascio di piani passanti per r è data da:

$$\lambda (x+z-2)+\mu(y-2z-1)=0 \iff \lambda x +\mu y +(\lambda -2\mu )z = 2\lambda +\mu$$

perché questo piano sia parallelo alla retta s, la sua normale dovrà essere ortogonale alla direzione di s e quindi

$$\langle (\lambda,\mu,\lambda-2\mu),(-1,2,-2)\rangle=0$$

ovvero

$$-3\lambda+6\mu=0 \iff \lambda = 2 \mu$$

Quindi il piano cercato ha equazione

2 x + y = 5.

    

Soluzione dell'esercizio 3  Le due coniche di equazioni rispettivamente x(x-1)=0 e y(x+y-2)=0 si intersecano esattamente nei quattro punti, quindi il fascio ha equazione $\alpha x(x-1)+ \beta y(x+y-2)=0$, ovvero

$$\alpha x^2 +\beta y^2 +\beta xy -\alpha x -2\beta y = 0.$$

La matrice associata alla conica è allora data da:

$$\left( \begin{array}{cc\vert c} \alpha & \frac{\beta}{2} & ... ...\\ \hline -\frac{\alpha}{2} & -\beta & 0 \end{array} \right)$$

Affinché la conica sia una parabola, dove essere non degenere e avere parte quadratica degenere. Questa seconda condizione è allora data da:

$$0=\det\left( \begin{array}{cc} \alpha & \frac{\beta}{2} \\ ... ...} & \beta \end{array} \right)=\beta(\alpha -\frac{\beta}{4}).$$

Per $\beta=0$ la conica si riduce a x(x-1)=0 che è degenere (sono due rette parallele). Per $\beta=4\alpha$, posto $\alpha=1$, la matrice della conica si riduce a

$$\left( \begin{array}{cc\vert c} 1 & 2 & -\frac{1}{2} \\ 2 & 4 & -4 \\ \hline -\frac{1}{2} & -4 & 0 \end{array} \right)$$

ed un semplice calcolo mostra che ha determinante pari a -9, e quindi la conica è non degenere e per tanto è una parabola.

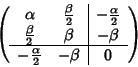
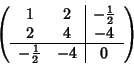
Per tre punti non allineati passa una e una sola circonferenza. È immediato verificare che la circonferenza passante per i punti P₁, P₂ e P₄ ha equazione x²+(y-1)²=1 e che quindi non contiene il punto P₃. Per tanto nel fascio delle coniche passanti per i 4 punti non possono esserci circonferenze. Alla stessa conclusione si poteva giungere analiticamente, osservando che la condizione affinché una conica sia una circonferenze (parte quadratica di tipo ax²+ay²), nel caso della conica del fascio, si riduce a $\alpha=\beta=0$.     

Soluzione dell'esercizio 4  Consideriamo i tre polinomi Q₁(x)=x²-1, Q₂(x)=x(x-1) e Q₃(x)=x(x+1). Li abbiamo scelti perché ognuno si annulla esattamente in due tra i punti -1,1,0. Se $P\in V^\perp$ allora

$$\begin{eqnarray*}0 & = & \langle P,Q_1\rangle = -4P(0)Q_1(0) = 4P(0) \\ 0 & = ... ... = 2P(-1) \\ 0 & = & \langle P,Q_3\rangle = P(1)Q_3(1) = 2P(1) \end{eqnarray*}$$

e quindi P(0)=P(1)=P(-1)=0, ma l'unico polinomio di grado minore o uguale a 2 con tre radici distinte è il polinomio identicamente nullo, quindi $V^\perp=\left\langle {}0\right\rangle$ e quindi $\langle,\rangle$ è non degenere.

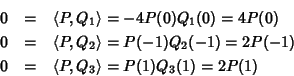
Osserviamo che i tre polinomi Q₁, Q₂ e Q₃ costituiscono anche una base ortogonale. Per come sono costruiti, comunque se ne fissino due diversi almeno uno dei due si annulla su 0, almeno uno si annulla su 1 e almeno uno si annulla su -1, quindi $\langle Q_i,Q_j\rangle=0$ogni volta che $i\ne j$. D'altra parte nessuno dei tre è il polinomio nullo ed è ben noto che $\dim V=3$.

La soluzione proposta fa uso di una scelta opportuna dei tre polinomi Q_i. Chiaramente si poteva partire dalla base standard di V data dai polinomi E₀(x)=1, E₁(x)=x e E₂(x)=x² ed esprimere la condizione di essere ortogonale a tutto lo spazio con $\langle P,E_i\rangle=0$, ottenendo in tal modo un sistema lineare nelle incognite P(0), P(1) e P(-1) che ammette solo la soluzione nulla.

Sempre a partire da tale base si poteva poi usare la costruzione standard (metodo di Jacobi) per ottenere una base ortogonale di V.     

Soluzione dell'esercizio 5  (i). Sia $v\in V$ esistono allora $u\in U$ e $w\in W$ tali che v=u+w. Ma allora

$$\langle v,v\rangle =\langle u+w,u+w\rangle= \langle u,u\rangle+\langle w,w\rangle+2\langle u,w\rangle=\langle u,u\rangle\ge0.$$

(ii). Siano $w_1,w_2\in W$ allora

$$0=\langle w_1+w_2,w_1+w_2\rangle=\langle w_1,w_1\rangle+\langle w_2,w_2\rangle+2\langle w_1,w_2\rangle=2\langle w_1,w_2\rangle$$

da cui la tesi.

(iii). Sia $v=u+w\in V^\perp$ con $u\in U$ e $w\in W$, allora

$$0=\langle v,u\rangle=\langle u+w,u\rangle=\langle u,u\rangle+\langle u,w\rangle=\langle u,u\rangle\Rightarrow u=0$$

quindi $v=w\in W$, ossia $V^\perp\subseteq W$.

D'altra parte se $w\in W$ e $v= u+ w'\in V$ si ha che

$$\langle w,v\rangle=\langle w,u\rangle+\langle w,w'\rangle=0+0=0$$

e quindi anche $W\subseteq V^\perp$, da cui la tesi.