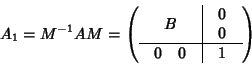Next: About this document ...
Up: Geometria 1
Previous: Geometria 1
Soluzione dell'esercizio 1 I punti Pi sono in posizione generale, infatti:
Una proiettività che porta i Pi sui Qi (risp. Ri) esiste se e solo se
i Qi (risp Ri) sono anch'essi in posizione generale ed in tal caso è
unica.
I Qi non sono in posizione generale, infatti
I punti Ri sono in posizione generale, infatti:
Determiniamo la proiettività tale che
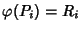 per ogni i. Poniamo
per ogni i. Poniamo
scriviamo v4 e w4 come combinazione lineare rispettivamente di
v1,v2,v3 e
w1,w2,w3.
l'applicazione lineare che porta
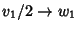 ,
,
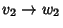 e
e
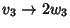 (e tutti i suoi multipli scalari) definisce la proiettività cercata.
(e tutti i suoi multipli scalari) definisce la proiettività cercata.
La matrice di tale applicazione lineare è data da:
la proiettività cercata è allora data da:

Soluzione dell'esercizio 2 Determiniamo equazioni parametriche della prima retta.
e quindi
La giacitura della retta r è generata dal vettore
v=(2,-2,1) mentre la
giacitura della retta s è generata dal vettore w=(0,0,1). v e w sono
evidentemente linearmente indipendenti, quindi per verificare che le rette sono
sghembe, basta vedere che non hanno punti in comune. Sostituendo l'espressione
parametrica della retta di s nell'equazione di r si vede immediatamente che
le due rette non hanno punti in comune (si ha che i punti di s sono tali che
x=y=1, mentre per i punti di r si ha x+y=1).
La giacitura dei due pioni sarà data dallo spazio generato da v e w, e
dovranno passare rispettivamente per un punto di r ed uno di s, quindi le
equazioni parametrichge dei due piani sono:
Dato che i due piani sono paralleli, la reciproca distanza è uguale alla
distanza di un punto di uno dei due piani dall'altro piano. Detto P=(1,1,0),
allora
d(H1,H2)=d(P,H1).
Determiniamo un'equazione implicita di H1. Il sistema nelle incognite
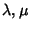 dato da
dato da
ha soluzione se e solo se
x + y -1 = 0, che è quindi l'equazione di H1.
Ma allora

Soluzione dell'esercizio 3 La matrice di 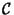 è
è
che è equivalente a
e quindi 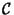 è una iperbole. La matrice di
è una iperbole. La matrice di
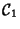 è
è
il determinante di tale matrice è -9/4 quindi è una conica non degenere,
la sua parte quadratica è degenere, quindi
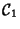 è una parabola. Non
esiste,per tanto, alcuna affinità che porti l'una sull'altra.
è una parabola. Non
esiste,per tanto, alcuna affinità che porti l'una sull'altra.
La matrice della conica
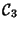 è:
è:
il determinante della matrice è 1 quindi la conica è non degenere. Il
determinante della parte quadratica è -1<0, quindi
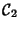 è
un'iperbole. Esiste quindi una affinità che porta
è
un'iperbole. Esiste quindi una affinità che porta 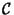 su
su
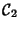 .
Determiniamone una.
.
Determiniamone una.
Osserviamo che
e quindi se (x,y) è un punto di 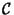 (ossia
x2-4y2-1=0), allora il punto
(ossia
x2-4y2-1=0), allora il punto
è un punto di
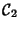 (ossia 2x'y'-1=0), quindi
(ossia 2x'y'-1=0), quindi 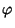 è l'affinità cercata.
è l'affinità cercata.

Soluzione dell'esercizio 4 Consideriamo le matrici
È noto che
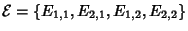 è una base di V; inoltre
è una base di V; inoltre
quindi  è una base ortogonale. Si osservi inoltre che
è una base ortogonale. Si osservi inoltre che
ossia  è una base ortonormale.
è una base ortonormale.
Si mostra in generale che, detta Ei,j la matrice 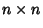 costituita da
tutti 0 tranne un 1 ol posto di riga i e colonna j, si ha che
costituita da
tutti 0 tranne un 1 ol posto di riga i e colonna j, si ha che
e quindi
ma ora
e quindi in definitiva
essia le matrici Ei,j costituiscono un abase ortonormale dello spazio delle
matrici 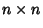 dotato di tale prodotto scalare.
dotato di tale prodotto scalare.

Soluzione dell'esercizio 5 Essendo una matrice reale 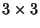 ,
A ha almeno un autovalore reale
,
A ha almeno un autovalore reale
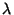 ,
ed in più, essendo una matrice ortogonale, necessariamente
,
ed in più, essendo una matrice ortogonale, necessariamente
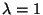 o
o
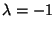 .
Dimostriamo che nelle nostre ipotesi 1è autovalore di A.
.
Dimostriamo che nelle nostre ipotesi 1è autovalore di A.
Se 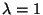 ,
non c'è niente da dimostrare. Se
,
non c'è niente da dimostrare. Se
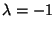 ,
sia v un autovettore unitario di A relativo all'autovalore -1.
Dato che A è ortogonale,
,
sia v un autovettore unitario di A relativo all'autovalore -1.
Dato che A è ortogonale,
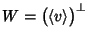 è invariante per
A; quindi, presa una base ortonormale
è invariante per
A; quindi, presa una base ortonormale
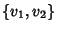 di W, la matrice
associata ad A rispetto alla base
di W, la matrice
associata ad A rispetto alla base
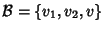 ha la forma
ha la forma
Inoltre, dato che 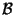 è una base ortonormale, la matrice di
cambiamento di base M è a sua volta ortogonale, quindi A1 è
ortogonale, da cui segue che anche B è ortogonale.
è una base ortonormale, la matrice di
cambiamento di base M è a sua volta ortogonale, quindi A1 è
ortogonale, da cui segue che anche B è ortogonale.
Poiché 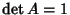 ,
si ha che
,
si ha che 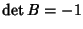 e quindi B è una riflessione ed
ha per tanto
due autovalori 1 e -1. Dato che gli autovalori di B sono anche
autovalori di A, 1 è un autovalore di A.
e quindi B è una riflessione ed
ha per tanto
due autovalori 1 e -1. Dato che gli autovalori di B sono anche
autovalori di A, 1 è un autovalore di A.
Nel ragionamento precedente possiamo allora supporre che 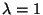 e quindi
esiste una base ortonormale in cui A assume la forma
e quindi
esiste una base ortonormale in cui A assume la forma
essendo B una matrice ortogonale con 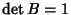 .
Ma allora B è della forma
.
Ma allora B è della forma
e quindi A risulta essere una rotazione attorno a
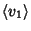 di un angolo
di un angolo
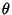 .
.
Osserviamo infine che A ed A1, essendo simili, hanno la stessa
traccia, quindi
da cui segue immediatamente la relazione richiesta, che determina a meno del
segno l'angolo 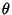 .
.




Next: About this document ...
Up: Geometria 1
Previous: Geometria 1
Domenico Luminati
1999-10-29
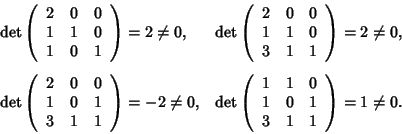
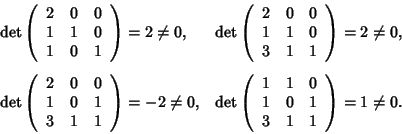
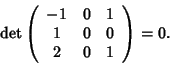
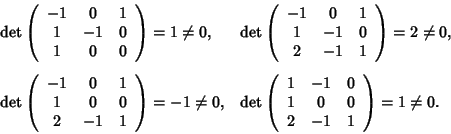
![]() per ogni i. Poniamo
per ogni i. Poniamo
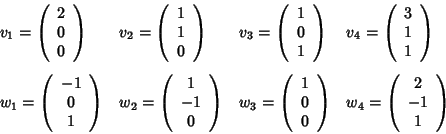
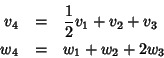
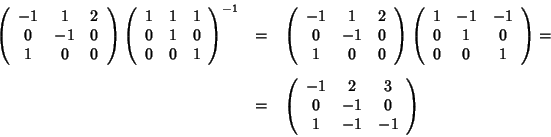
![\begin{eqnarray*}\varphi([x_0,x_1,x_2]) & = &
\left[
\left(
\begin{array}{ccc...
... =
\\ [10pt]
& = &
\left[3x_2+2x_1-x_0,x_1,x_0-x_1-x_2\right]
\end{eqnarray*}](img31.gif)
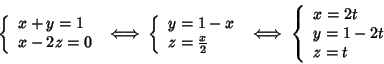
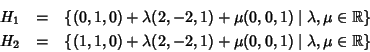
![]() dato da
dato da
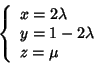
![]() è
è
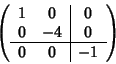
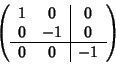
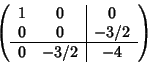
![]() è:
è:

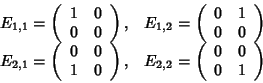
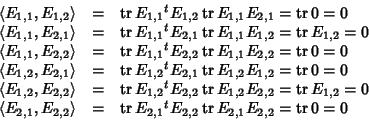
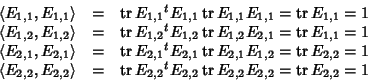
![]() costituita da
tutti 0 tranne un 1 ol posto di riga i e colonna j, si ha che
costituita da
tutti 0 tranne un 1 ol posto di riga i e colonna j, si ha che
![]() ,
A ha almeno un autovalore reale
,
A ha almeno un autovalore reale
![]() ,
ed in più, essendo una matrice ortogonale, necessariamente
,
ed in più, essendo una matrice ortogonale, necessariamente
![]() o
o
![]() .
Dimostriamo che nelle nostre ipotesi 1è autovalore di A.
.
Dimostriamo che nelle nostre ipotesi 1è autovalore di A.
![]() ,
non c'è niente da dimostrare. Se
,
non c'è niente da dimostrare. Se
![]() ,
sia v un autovettore unitario di A relativo all'autovalore -1.
Dato che A è ortogonale,
,
sia v un autovettore unitario di A relativo all'autovalore -1.
Dato che A è ortogonale,
![]() è invariante per
A; quindi, presa una base ortonormale
è invariante per
A; quindi, presa una base ortonormale
![]() di W, la matrice
associata ad A rispetto alla base
di W, la matrice
associata ad A rispetto alla base
![]() ha la forma
ha la forma
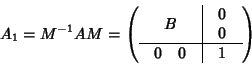
![]() ,
si ha che
,
si ha che ![]() e quindi B è una riflessione ed
ha per tanto
due autovalori 1 e -1. Dato che gli autovalori di B sono anche
autovalori di A, 1 è un autovalore di A.
e quindi B è una riflessione ed
ha per tanto
due autovalori 1 e -1. Dato che gli autovalori di B sono anche
autovalori di A, 1 è un autovalore di A.
![]() e quindi
esiste una base ortonormale in cui A assume la forma
e quindi
esiste una base ortonormale in cui A assume la forma