


Next: About this document ...
Up: Geometria 1
Previous: Geometria 1
Soluzione dell'esercizio 1 Siano
Un semplice calcolo mostra che
quindi sia v1,v2 che w1,w2 sono linearmente indipendenti, e pertanto
l'affinità cercata esiste ed è unica. Cominciamo determinando la parte
lineare. Questa è un'applicazione tale che
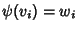 per i=1,2. Ma
allora è data dato che la matrice (v1|v2), ottenuta affiancando v1 e
v2, porta i vettori della base standard di
per i=1,2. Ma
allora è data dato che la matrice (v1|v2), ottenuta affiancando v1 e
v2, porta i vettori della base standard di
 su v1 e v2,
l'applicazione
su v1 e v2,
l'applicazione  sarà definita dalla matrice
sarà definita dalla matrice
La parte di traslazione è infine data da
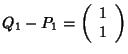 e quindi l'affinità cercata è:
e quindi l'affinità cercata è:
La parte lineare è data da una matrice ortogonale e
quindi 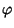 è una isometria inoltre il determinante di tale maice è 1quindi o ùna rotazioe o una traslazione. Dato che evidentemente non è una
traslazione (la parte lineare non è l'identità),
è una isometria inoltre il determinante di tale maice è 1quindi o ùna rotazioe o una traslazione. Dato che evidentemente non è una
traslazione (la parte lineare non è l'identità), 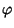 è una rotazione.
è una rotazione.

Soluzione dell'esercizio 2 Il generico piano passante per P è dato dall'equazione
a(x-1)+b(y-1)+c(z-2)=0.
Perché tale piano sia parallelo ad r deve risultare che il vettore
direzione della retta, che è il vettore
v=(1,-1,2), sia perpendicolare
al vettore (a,b,c) perpendicolare al piano, ossia
a-b+2c=0.
Affinché il piano sia perpendicolare al piano H1 deve essere che i
vettori normali ai due piani siano tra loro ortogonali, dato che il vettore
normale ad H1 è (1,2,1) deve aversi
a+2b+c=0.
mettendo insieme le due condizioni trovate si ottiene il sistema lineare
cha ha per soluzione
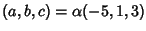 con
con
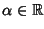 .
Dato che
tali soluzioni sono uniche a meno di moltiplicazione per una costante (sono
uno spazio vettoriale di dimensione 1), il piano H2 esiste ed è
unico. Una sua equazione è data da:
.
Dato che
tali soluzioni sono uniche a meno di moltiplicazione per una costante (sono
uno spazio vettoriale di dimensione 1), il piano H2 esiste ed è
unico. Una sua equazione è data da:
Se esistesse il piano H3 allora H1 dovrebbe essere perpendicolare alla
retta r, dato che H1 è parallelo ad H3 che è perpendicolare a
r. Quindi il vettore direzione della retta r dovrebbe essere linearmente
dipendente dal vettore normale del piano H1. Ma i vettori (1,-1,2) e
(1,2,1) sono linearmente indipendenti: il minore dato dall eprime due
colonne della matrice
ha determinante 3 e quindi le righe della matrice sono linearmente
indipendenti.

Soluzione dell'esercizio 3 Le rette passnti per P1, P2 e per P2, P3 sono rispettivamente date
dalle equazioni x=0 e x-2=0, che insieme formano la conica di equazione
x(x-2)=0. Le rette passanti per P1, P4 e per P2, P3 sono
rispettivamente date dalle equazioni y-3=0 e y-2=0, che insieme formano la
conica di equazione
(y-2)(y-3)=0. Poiché l'intersezione di queste due
coniche è data dai quattro punti
P1,P2,P-3,P4, una equazione del fascio
di coniche cercato è data da:
Affinché una conica del fascio passi per P5=(1,1) dovrà essere che
ossia
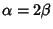 e quindi
e quindi
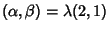 .
Dato che la
soluzione è unica a meno di moltiplicazione per una costante, si ha che
esiste una unica conica del fascio passante per P5 e una sua equazione si
ottiene per
.
Dato che la
soluzione è unica a meno di moltiplicazione per una costante, si ha che
esiste una unica conica del fascio passante per P5 e una sua equazione si
ottiene per 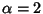 e
e 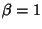 ossia è
ossia è
2x2+y2-4x-5y+6=0.
Studiamo questa conica. La matrice associata è data da:
La parte quadratica è definita positiva (è diagonale con due autovalori
positivi), quindi si hanno tre possibilità o è un'ellisse (forma canonica
x2+y2-1=0), oppure è vuota (forma canonica
x2+y2+1=0), oppure è un
punto (forma canonica x2+y2=0). Dato che la nostra conica contiene 5punti, può soltanto essere un'ellisse.

Soluzione dell'esercizio 4 Indichiamo con ei i vettori della base standard di
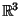 e con
e con
 il prodotto scalare definito dalla matrice. Osserviamo che
il prodotto scalare definito dalla matrice. Osserviamo che
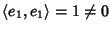 ,
quindi possiamo fare il seguente cambiamento
di base:
,
quindi possiamo fare il seguente cambiamento
di base:
Per costruzione v2 e v3 sono ortognali a v1 inoltre:
quindi la matrice del prodotto scalare rispetto a questa base è data da:
Dato che
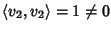 possiamo iterare il procedimento e
considerare la base
possiamo iterare il procedimento e
considerare la base
Per costruzione questa è una base ortogonale e
e quindi la matrice associata rispetto a questa base è data da:
Quindi l'indice di positività del prodotto scalare è 2, l'indice di
negatività è 1 e l'indice di nullità è 0.
Scriviamo esplicitamente la base ortogonale che abbiamo trovato:

Soluzione dell'esercizio 5 Sia
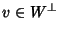 e proviamo che allora
e proviamo che allora
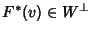 .
Se
.
Se 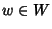 allora
allora
dato che
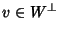 e
e 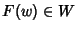 (si usa qui l'ipotesi che
(si usa qui l'ipotesi che
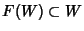 ). Ma allora per l'arbitrarietà di
). Ma allora per l'arbitrarietà di 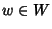 si ha che
si ha che
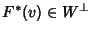 e quindi, per l'arbitrarietà di
e quindi, per l'arbitrarietà di
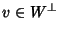 ,
,
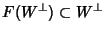 .
.




Next: About this document ...
Up: Geometria 1
Previous: Geometria 1
Domenico Luminati
1999-10-29
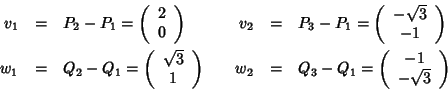
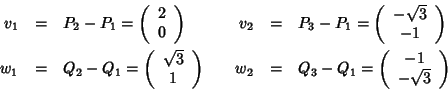
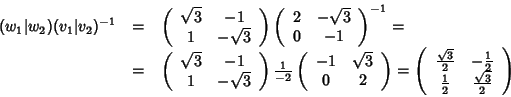
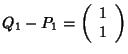 e quindi l'affinità cercata è:
e quindi l'affinità cercata è:
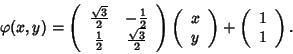
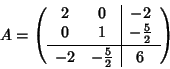
![]() e con
e con
![]() il prodotto scalare definito dalla matrice. Osserviamo che
il prodotto scalare definito dalla matrice. Osserviamo che
![]() ,
quindi possiamo fare il seguente cambiamento
di base:
,
quindi possiamo fare il seguente cambiamento
di base:
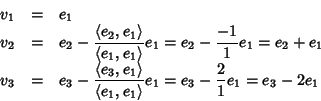
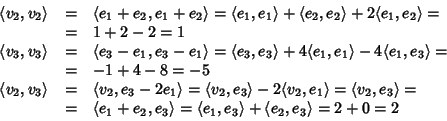
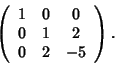
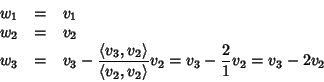
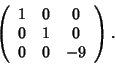
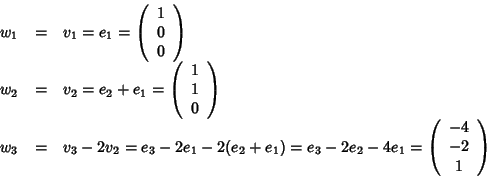
![]() e proviamo che allora
e proviamo che allora
![]() .
Se
.
Se ![]() allora
allora