Implementation

It is convenient to work in the coordinate representation, as this representation is the most natural for writing the interaction potential and external potential. In a system of $N$ particles in $D$ dimensions the distribution function depends on $D N$ variables $p({\bf R}) = p({\vec r}_1, ..., {\vec r}_N)$. An average value of an operator $\hat A$ is then given by a $D N$-multidimensional integral

$$\langle A\rangle = \frac{\int...\int A({\vec r}_1,...,{\vec r}_N)... ....\vec{dr_N}}{\int...\int p({\vec r}_1,...,{\vec r}_N)) \vec{dr_1}...\vec{dr_N}}$$ (2.3)

Even for a few particles $N\approx 10$ the structure of the integral becomes too difficult for implementation usual discretization methods of integration and instead one can use stochastic Monte Carlo methods. The idea of the method is to generate a set of states (chain) ${\vec r_1},...,{\vec r}_M$ with the probability distribution $p({\bf R})$ and approximate the $\langle A\rangle$ as the average

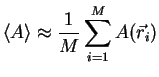$$\langle A\rangle \approx \frac{1}{M}\sum\limits_{i=1}^M A({\vec r}_i)$$ (2.4)

Such a chain where the next configuration ${\bf R}'$ depends only on the previous configuration ${\bf R}$ (Markov chain) can be generated by the Metropolis algorithm [MRR+53]: the new configuration is accepted with the probability $P({\bf R} \rightarrow {\bf R}')$ given by the rule

$$P({\bf R}\rightarrow {\bf R}') = \left\{ \begin{tabular}{ccc} $1$... ...\bf R}')/p({\bf R})$, & if $p({\bf R}') < p({\bf R})$\ \\ \end{tabular}\right.$$ (2.5)

In a quantum system the probability distribution is given by the square of the wave function module as Eq. 2.1. The specific construction of wave functions will be discussed in Sec. 2.5.

The efficiency significantly depends on the type of the trial moves. A natural way to generate a new configuration is to move all particles ${\vec r}_i' = {\vec r}_i+\vec\xi_i, i=\overline{1,N}$, here $\vec\xi_i$ is a random shift delimited to range $\vert\vec\xi_i\vert<\Xi$. If the amplitude of the shift $\Xi$ is too large the acceptance rate becomes too small, if instead $\Xi$ is very small, almost all moves are accepted, but the generated configurations are strongly correlated. The acceptance rate of about $50\%$ in general provides a good choice.

The efficiency of a variational calculation can be highly improved by doing a complex move consisting of separate moves of one particle at a time. Each independent move allow a larger displacement at the fixed acceptance rate. Indeed, the amplitude of each individual move can be an order of magnitude larger and consequently leading to a faster convergence of the sampling.