



Next: Spazi vettoriali
Up: Esercizi
Previous: Matrici
Indice
Esercizio 15
Determinare le soluzioni del seguente sistema omogeneo:
Dimostrazione.
La matrice completa associata al sistema è:
Riduciamo la matrice a gradino. Una possibile riduzione per righe è
Il sistema associato all'ultima matrice è:
che anmmette l'unica soluzione:
In modo alternativo si può precedere come segue. La matrice dei coefficienti
associata al sistema è la matrice:
Il determinante di

è uguale a :
Ne segue che la matrice

ha rango

così come la matrice completa associata al
sistema. Per il teorema di Rouchè-Capelli il sistema ha una unica soluzione. D'altra
parte ogni sistema omogeneo ha almeno la soluzione banale, pertanto la soluzione è:

Esercizio 16
Determinare, se esistono, le soluzioni del seguente sistema non omogeneo:
Dimostrazione.
La matrice completa associata al sistema è la matrice:
Una possibile riduzioone a gradino è:
Il rango della matrice incompleta è

mentre il rango della matrice completa è

.
Il sistema non ha soluzioni.
D'altra parte, nel sistema associato all'ultima matrice, l'ultima riga corrisponde
all'equazione
manifestamente falsa.

Esercizio 17
Determinare, se esistono, le soluzioni del seguente sistema non omogeneo:
Dimostrazione.
La matrice completa associata al sistema è:
Una possibile riduzione a gradino è :
Il rango della matrice dei coefficienti è uguale al rango della matrice completa e pari a

. Dal teorema di Rouchè-Capelli segue che il sistema ammette infinite soluzioni.
Per determinare le soluzioni scriviamo il sistema associato alla matrice ridotta:
Risolvendo in funzione della variabile

, si ottiene:
Posto

, con

, le soluzioni si riscrivono:

Esercizio 18
Determinare, se esistono, le soluzioni del seguente sistema non omogeneo:
Dimostrazione.
La matrice completa associata al sistema è la matrice:
Per ridurre la matrice a gradino scambiamo la prima e la seconda colonna, ottenendo
così la matrice:
Notiamo che l'aver scambiato le prime due colonne colonne della matrice implica che
l'ordine scelto per le variabili, nello scrivere il sistema associato, diventa

,

,

.
Una possibile riduzione per righe è:
Il rango della matrice completa è uguale al rango della matrice incompleta e uguale a

. Il sistema allora ammette una unica soluzione.
Per determinare la soluzione scriviamo, ricordando che abbiamo scambiato le prime due
colonne, il sistema associato alla matrice ridotta:
La soluzione è:

Esercizio 19
Discutere l'esistenza di soluzioni per il seguente sistema lineare, al variare del parametro reale

.
Determinare, ove esistano, le soluzioni.
Dimostrazione.
La matrice completa associata al sistema è:
Una possibile riduzione per righe è:
Notiamo che la riduzione fatta ha senso per ogni valore del parametro reale

. Infatti
nell'ultimo passaggio abbiamo sostituito la seconda riga con

volte la prima riga meno
la seconda riga. Se

quello che abbiamo fatto è sostituire la seconda riga con un
suo multiplo non nullo.
Stesso discorso vale per la terza riga, infatti questa è stata sostituita con

volte la prima riga meno la terza.
Se

di nuovo abbiamo sostituito la terza riga con un suo multiplo non nullo.
Ultimiamo ora la riduzione:
Per

la matrice incompleta e la matrice completa hanno entrambe rango

pertanto il sistema ammette una sola soluzione.
La soluzione è:
Se

la matrice ridotta diventa:
La matrice completa e incompleta hanno entrambe rango

pertanto il sistema ammette
infinite soluzioni:
Infine per

la matrice ridotta diventa:
e il sistema non ha soluzioni.

Esercizio 20
Discutere l'esistenza di soluzioni per il seguente sistema lineare, al variare del parametro reale

.
Determinare, ove esistano, le soluzioni.
Dimostrazione.
La matrice dei coefficienti del sistema è:
Calcoliamo il determinante di

:
Per

la matrice

ha rango

e dunque il sistema ammette solo la
soluzione banale:
Se

la matrice dei coefficienti diventa:
che si vede facilmente avere rango

. Un minore di ordine due non nullo è, per
esempio, il
minore
Ne segue che il sistema ammette infinite soluzioni. Le soluzioni si determinano
risolvendo il sistema
da cui:
Per

la matrice dei coefficienti del sistema è :
Di nuovo la matrice ha rango

e il sistema ammette infinite soluzioni:
Infine se

la matrice dei coefficienti diventa:
Le soluzioni sono:

Esercizio 21
Discutere l'esistenza di soluzioni per il seguente sistema lineare, al variare del parametro
reale

.
Determinare, ove esistano, le soluzioni.
Dimostrazione.
La matrice dei coefficienti del sistema è:
Il suo determinante risulta essere
sicchè per

si ha una e una sola soluzione del sistema.
La soluzione, che si può determinare per esempio con il metodo di Cramer, è
Per

la matrice completa associata al sistema diventa:
che si può ridurre come segue:
Si hanno infinite soluzioni del sistema :
Infine per

la matrice completa associata al sistema diventa:
Una possibile riduzione è:
Segue che il sistema non ammette in questo caso alcuna soluzione.

Esercizio 22
Discutere l'esistenza di soluzioni per il seguente sistema lineare, al variare del parametro reale

.
Determinare, ove esistano, le soluzioni.
Dimostrazione.
La matrice completa associata al sistema è la matrice:
Una possibile riduzione per righe è la seguente:
Per

la matrice completa e la matrice incompleta hanno entrambe rango

e il
sistema ammette una unica soluzione.
La soluzione è :
Per

la matrice ridotta diventa:
da cui si deduce facilmente che il sistema non ha soluzioni per

.
Per 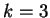 invece la matrice ridotta si riscrive:
invece la matrice ridotta si riscrive:
In questo caso la matrice completa e incompleta hanno entrambe rango

. Il sistema
ammette le infinite soluzioni seguenti:

Esercizio 23
Discutere l'esistenza di soluzioni per il seguente sistema lineare, al variare del parametro reale

.
Determinare, ove esistano, le soluzioni.
Dimostrazione.
La matrice dei coefficienti del sistema è:
il cui determinante è pari a:
Per

il sistema ammette una e una sola soluzione . Determiniamo la soluzione utilizzando
la regola di Cramer.
Risulta:
Per

la matrice completa del sistema è
Si vede facilmente che la matrice completa e la matrice incompleta hanno entrambe rango

.
Il sistema ammette infinite soluzioni che sono le soluzioni dell'equazione
Risulta allora:
Se

la matrice completa del sistema diventa:
Riduciamo la matrice a gradino:
Segue che, per

, il sistema non ammette alcuna soluzione.

Esercizio 24
Discutere l'esistenza di soluzioni per il seguente sistema lineare, al variare del parametro reale

.
Determinare, ove esistano, le soluzioni.
Dimostrazione.
La matrice completa associata al sistema è la matrice:
Una possibile riduzione è la seguente:
Ora scambiamo la seconda e la terza colonna cambiando così l'ordine delle variabili in

,

e

.
Otteniamo:
Per

il sistema ammette una sola soluzione:
Per

, invece, non esistono soluzioni.

Esercizio 25
Determinare i valori del parametro reale

tali che il sistema
abbia, rispettivamente, una unica soluzione, nessuna soluzione o
più di una soluzione.
Dimostrazione.
Il determinante della matrice dei coefficienti è pari a

, sicchè per

il sistema
ammette una unica soluzione. Se
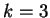
la matrice completa associata al sistema è la matrice:
Si vede facilmente che la prima riga è uguale alla seconda riga meno la terza e, d'altra parte la
seconda e la terza riga non sono tra loro proporzionali. Ne segue che, per
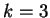
, il sistema ammette
infinite soluzioni.





Next: Spazi vettoriali
Up: Esercizi
Previous: Matrici
Indice
Andreatta Marco
2000-09-18















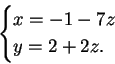








































![]() invece la matrice ridotta si riscrive:
invece la matrice ridotta si riscrive:


















